题目内容
15.设函数f(x)=$\left\{\begin{array}{l}{{2}^{-x},x≤0}\\{{x}^{\frac{1}{2}}-1,x>0}\end{array}\right.$,如果f(a)>1,求a的取值范围(-∞,0)∪(4,+∞).分析 根据已知中分段函数的解析式,分类讨论满足f(a)>1的a的取值范围,综合讨论结果,可得答案.
解答 解:当a≤0时,解f(a)=2-a>1得:a∈(-∞,0),
当a>0时,解f(a)=${a}^{\frac{1}{2}}-1$>1得:a∈(4,+∞),
综上所述,a∈(-∞,0)∪(4,+∞),
故答案为:(-∞,0)∪(4,+∞)
点评 本题考查的知识点是分段函数的应用,分类讨论思想,指数不等式的解法,难度中档.

练习册系列答案
相关题目
3.已知f(x)=$\left\{\begin{array}{l}{x+1(x<0)}\\{-x-1(x≥0)}\end{array}\right.$则不等式x+(x+1)•f(x-1)≤3的解集是( )
| A. | {x|x≥-3} | B. | {x|x≥1} | C. | {x|-3≤x≤1} | D. | {x|x≥1或x≤-3} |
4.在等差数列{an}中,若a1004+a1006+a1008=9,则该数列的前2011项的和为( )
| A. | 6033 | B. | 6030 | C. | 2011 | D. | 2010 |
1.若f(x)对于任意实数x恒有2f(x)-f(-x)=3x+1,则f(1)=( )
| A. | 2 | B. | 0 | C. | 1 | D. | -1 |
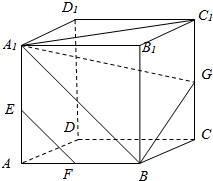 在正方体AC1中.
在正方体AC1中.