题目内容
已知函数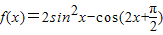 .
.(Ⅰ)求
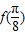 的值;
的值;(Ⅱ)求函数f(x)的最小正周期及单调递增区间.
【答案】分析:(Ⅰ)利用两角和差的正弦公式、二倍角公式化简函数的解析式为f(x)=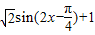 ,由此求得
,由此求得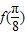 的值.
的值.
(Ⅱ)根据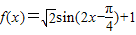 ,求出它的最小正周期,令
,求出它的最小正周期,令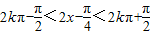 ,求出x的范围,即可得到单调递增区间.
,求出x的范围,即可得到单调递增区间.
解答:解:(Ⅰ)因为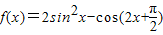 =2sin2x+sin2x…(2分)
=2sin2x+sin2x…(2分)
=1-cos2x+sin2x…(4分)
=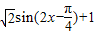 …(6分)
…(6分)
所以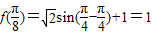 .…(7分)
.…(7分)
(Ⅱ)因为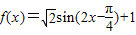 ,所以,最小正周期等于
,所以,最小正周期等于 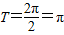 .…(9分)
.…(9分)
又y=sinx的单调递增区间为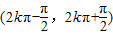 ,(k∈Z),…(10分)
,(k∈Z),…(10分)
所以令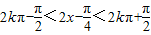 ,…(11分)
,…(11分)
解得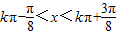 …(12分)
…(12分)
所以函数f(x)的单调增区间为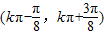 ,(k∈Z).…(13分)
,(k∈Z).…(13分)
点评:本题主要考查两角和差的正弦公式、二倍角公式的应用,正弦函数的周期性以及单调性,属于中档题.
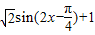 ,由此求得
,由此求得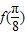 的值.
的值.(Ⅱ)根据
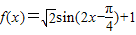 ,求出它的最小正周期,令
,求出它的最小正周期,令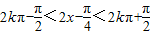 ,求出x的范围,即可得到单调递增区间.
,求出x的范围,即可得到单调递增区间.解答:解:(Ⅰ)因为
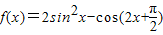 =2sin2x+sin2x…(2分)
=2sin2x+sin2x…(2分)=1-cos2x+sin2x…(4分)
=
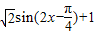 …(6分)
…(6分)所以
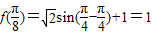 .…(7分)
.…(7分)(Ⅱ)因为
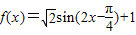 ,所以,最小正周期等于
,所以,最小正周期等于 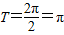 .…(9分)
.…(9分)又y=sinx的单调递增区间为
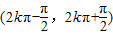 ,(k∈Z),…(10分)
,(k∈Z),…(10分)所以令
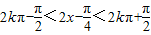 ,…(11分)
,…(11分)解得
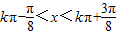 …(12分)
…(12分)所以函数f(x)的单调增区间为
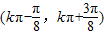 ,(k∈Z).…(13分)
,(k∈Z).…(13分)点评:本题主要考查两角和差的正弦公式、二倍角公式的应用,正弦函数的周期性以及单调性,属于中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
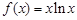 .
.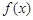 的最小值;
的最小值;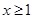 都有
都有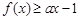 ,求实数
,求实数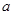 的取值范围.
的取值范围.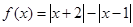
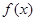 的值域;
的值域;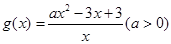 ,若对
,若对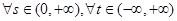 恒有
恒有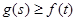 成立,试求实数
成立,试求实数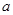 的取值氛围。
的取值氛围。 ,(1)求
,(1)求 的定义域;
的定义域; 是第四象限的角,且
是第四象限的角,且 ,求
,求 的值。
的值。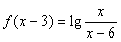 ,
,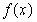 的解析式;
的解析式; .
.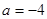 时,求
时,求 的最小值;
的最小值;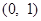 上为单调函数,求实数
上为单调函数,求实数 的取值范围;
的取值范围;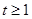 时,不等式
时,不等式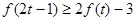 恒成立,求实数
恒成立,求实数