题目内容
若平面向量 =(1,-2)与
=(1,-2)与 的夹角是180°,且
的夹角是180°,且 ,则
,则 等于( )
等于( )A.(-6,3)
B.(3,-6)
C.(6,-3)
D.(-3,6)
【答案】分析:由于平面向量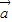 =(1,-2)与
=(1,-2)与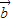 的夹角是180°,故
的夹角是180°,故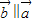 且与
且与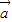 反向.可设
反向.可设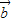 =(x,y)则根据
=(x,y)则根据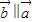 可得y+2x=0①,根据
可得y+2x=0①,根据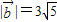 可得
可得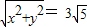 ②再由①②解出x,y再根据
②再由①②解出x,y再根据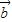 与
与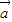 反向即可得出符合条件的
反向即可得出符合条件的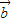 .
.
解答:解:∵平面向量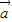 =(1,-2)与
=(1,-2)与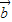 的夹角是180°
的夹角是180°
∴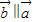 且与
且与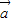 反向
反向
设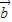 =(x,y)
=(x,y)
∵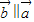 ,
,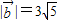
∴y+2x=0①,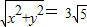 ②
②
∴由①②得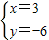 或
或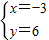
∵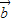 与
与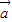 反向
反向
∴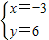
∴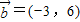
故选D
点评:本题主要考察了平行或共线向量的坐标表示、模的坐标计算,属常考题型,较难.解题的关键是根据平面向量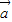 =(1,-2)与
=(1,-2)与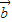 的夹角是180°分析出
的夹角是180°分析出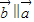 且与
且与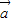 反向(此结论非常重要,否则会产生增根),同时熟记两向量平行以及向量模的坐标计算公式!
反向(此结论非常重要,否则会产生增根),同时熟记两向量平行以及向量模的坐标计算公式!
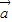 =(1,-2)与
=(1,-2)与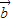 的夹角是180°,故
的夹角是180°,故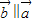 且与
且与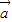 反向.可设
反向.可设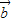 =(x,y)则根据
=(x,y)则根据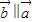 可得y+2x=0①,根据
可得y+2x=0①,根据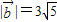 可得
可得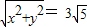 ②再由①②解出x,y再根据
②再由①②解出x,y再根据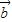 与
与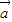 反向即可得出符合条件的
反向即可得出符合条件的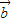 .
.解答:解:∵平面向量
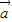 =(1,-2)与
=(1,-2)与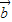 的夹角是180°
的夹角是180°∴
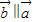 且与
且与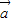 反向
反向设
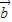 =(x,y)
=(x,y)∵
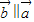 ,
,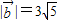
∴y+2x=0①,
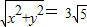 ②
②∴由①②得
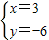 或
或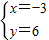
∵
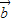 与
与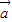 反向
反向∴
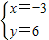
∴
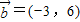
故选D
点评:本题主要考察了平行或共线向量的坐标表示、模的坐标计算,属常考题型,较难.解题的关键是根据平面向量
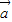 =(1,-2)与
=(1,-2)与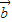 的夹角是180°分析出
的夹角是180°分析出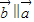 且与
且与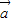 反向(此结论非常重要,否则会产生增根),同时熟记两向量平行以及向量模的坐标计算公式!
反向(此结论非常重要,否则会产生增根),同时熟记两向量平行以及向量模的坐标计算公式! 
练习册系列答案
相关题目
若平面向量
=(-1,2)与
的夹角是180°,且|
|=3
,则
坐标为( )
| a |
| b |
| b |
| 5 |
| b |
| A、(6,-3) |
| B、(-6,3) |
| C、(-3,6) |
| D、(3,-6) |
若平面向量
=(1,x)和
=(2x+3,-x)互相平行,其中x∈R,则|
-
|=( )
| a |
| b |
| a |
| b |
A、2
| ||
B、2或2
| ||
| C、-2或0 | ||
| D、2或10 |