题目内容
【题目】在四棱锥
中，侧面
底面
，底面为直角梯形，
∥
，
，
，
，
，
为的中点，
为
的中点。
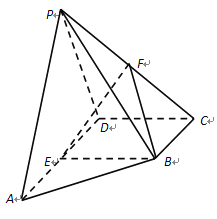
（1）求证：
∥平面
；
（2）求二面角
的余弦值。
【答案】(1)见证明；(2)
【解析】
（1）利用面外线与面内线平行证明面外线平行于平面。
（2）建立空间直角坐标系，利用两个半平面的法向量的夹角余弦值，来求二面角的平面角的余弦值，或用几何法找到二面角的平面角来求余弦值。
（1）连接
交
于
，并连接
，
，
，
，
为
中点，
，且
，
四边形
为平行四边形，
为中点，又
为
中点，
，
平面
，
平面，
平面.
（2）〖解法1〗（向量法）连接
，由E为AD的中点及
，
得
则
，∵侧面
底面
，且交于，
∴
面，
如图所示，以E为原点，EA、EB、EP分别为
x、y、z轴建立空间直角坐标系，
则
，
，
，C
.
∵为的中点，∴F
∴
，
设平面EBF法向量为
，则
,
取
,
平面EBA法向量可取：
,
设二面角F-BE-A的大小为
，显然为钝角，
∴
,
∴二面角F-BE-A的余弦值为
（2）〖解法2〗（几何法1）连接，
由E为AD的中点及，
得
∵
，
取
中点
，连
，
，
，
侧面底面，且交于，
，
∴
面
∵ 
面 
面
∴
∵为的中点，为的中点
，
∴
∴∠MEA为二面角F-BE-A的平面角
在
中，
，
在
中，由余弦定理得
∴在
中，由余弦定理得cos∠MEA
，
所以二面角F-BE-A的余弦值为.
（2）〖解法3〗（几何法2）连接，由E为AD的中点及，
得
侧面底面，∴面，
∵
，
连
交于点
，则为中点，连
，
，，
∵为的中点，∴
，
面，
又
，∴
∴ 
∴∠FNQ为二面角F-BE-A的平面角的补角
在
中，
，
由勾股定理得
∴cos∠FNQ
，
所以二面角F-BE-A的余弦值为.
【题目】高中生在被问及“家，朋友聚集的地方，个人空间”三个场所中“感到最幸福的场所在哪里？”这个问题时，从中国某城市的高中生中，随机抽取了55人，从美国某城市的高中生中随机抽取了45人进行答题.中国高中生答题情况是：选择家的占
、朋友聚集的地方占
、个人空间占.美国高中生答题情况是：朋友聚集的地方占
、家占
、个人空间占.如下表：
在家里最幸福 | 在其它场所幸福 | 合计 | |
中国高中生 | |||
美国高中生 | |||
合计 |
（Ⅰ）请将
列联表补充完整；试判断能否有
的把握认为“恋家”与否与国别有关；
（Ⅱ）从被调查的不“恋家”的美国学生中，用分层抽样的方法选出4人接受进一步调查，再从4人中随机抽取2人到中国交流学习，求2人中含有在“个人空间”感到幸福的学生的概率.
附：
，其中
.
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.828 |
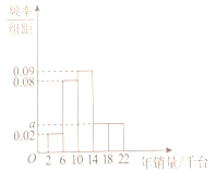
【题目】为推动文明城市创建，提升城市整体形象，2018年12月30日盐城市人民政府出台了《盐城市停车管理办法》，2019年3月1日起施行.这项工作有利于市民养成良好的停车习惯，帮助他们树立绿色出行的意识，受到了广大市民的一致好评.现从某单位随机抽取80名职工，统计了他们一周内路边停车的时间
（单位：小时），整理得到数据分组及频率分布直方图如下：
组号 | 分组 | 频数 |
1 |
| 6 |
2 |
| 8 |
3 |
| 22 |
4 |
| 28 |
5 |
| 12 |
6 |
| 4 |
（1）从该单位随机选取一名职工，试计算这名职工一周内路边停车的时间少于8小时的频率；
（2）求频率分布直方图中
的值.
