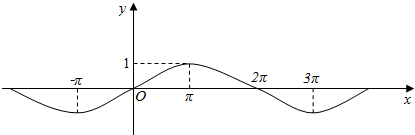
题目内容
13．设$\overrightarrow{e_1}，\overrightarrow{e_2}$是两个不共线的向量，实数x，y满足$（3x-4y）\overrightarrow{e_1}+（2x-3y）\overrightarrow{e_2}=6\overrightarrow{e_1}+3\overrightarrow{e_2}$，则x+y=9．分析 根据两向量相等，对应的系数相等，列出方程组，求出x、y的值即可．
解答 解：根据向量相等的定义，得
$\left\{\begin{array}{l}{3x-4y=6}\\{2x-3y=3}\end{array}\right.$，
解得x=6，y=3；
∴x+y=9．
故答案为：9．
点评 本题考查了平面向量的相等的概念与应用问题，是基础题目．
练习册系列答案
相关题目
3．下列不等式恒成立的是（ ）
| A． | ex＜1+x（x≠0） | B． | sinx＜x（x∈（0，π）） | C． | lnx＞x（x＞0） | D． | x＞ex（x＞0） |
8．已知点O是△ABC的外接圆圆心，且AB=3，AC=4．若存在非零实数x、y，使得$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}$，且x+2y=1，则cos∠BAC的值为（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $\frac{{\sqrt{2}}}{3}$ | D． | $\frac{1}{3}$ |
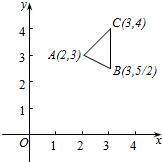已知点（x，y）在△ABC所包围的阴影区域内（包含边界），若B是使得z=ax-y取得最大值的最优解，则实数a的取值范围为[-$\frac{1}{2}$，+∞）．
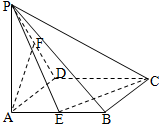如图，四棱锥P-ABCD的底面为正方形，PA⊥底面ABCD，E、F分别为AB、PD的中点．