题目内容

求证：logxy•logyz•logzx=1．
考点：对数的运算性质
专题：函数的性质及应用
分析：直接利用换底公式证明即可．
解答： 证明：由换底公式可得：logxy•logyz•logzx=
lgy
lgx
•
lgz
lgy
•
lgx
lgz
=1．
等式成立．
点评：本题考查对数的运算法则的应用，考查计算能力．
练习册系列答案
相关题目
在直角坐标系xOy中，圆C1和C2的参数方程分别是
x=2+2cosφ
y=2sinφ
（φ为参数）和
x=cosφ
y=1+sinφ
（φ为参数），以O为极点，x轴的正半轴为极轴建立极坐标系．
（1）求圆C1和C2的极坐标方程；
（2）射线OM：θ=a与圆C1的交点为O、P，与圆C2的交点为O、Q，求|OP|•|OQ|的最大值．
证明：x2-x＞lnx，x∈（0，1）
曲线f（x）=
x2+a
x+1
在点（1，f（1））处切线的倾斜角为
3π
4
，则实数a=（　　）
A、1B、-1C、7D、-7
已知α为第四象限角，tanα=-
1
2
，那么5 |log5cosα|=
 
．
已知椭圆
x2
9
+
y2
m
=1与双曲线
x2
9
-
y2
n
=1的离心率是方程9x2-18x+8=0的两根，mn=
 
．
数列{an}的前n项和Sn=2n2-5n（n∈N+），则数列{（n-4）an}中数值最小的项是第（　　）项．
A、6B、5C、4D、3
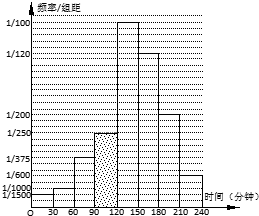为了调查学生星期天晚上学习时间利用问题，某校从高二年级100名学生（其中走读生450名，住宿生550名）中，采用分层抽样的方法抽取n名学生进行问卷调查，根据问卷取得了这n名同学每天晚上学习时间（单位：分钟）的数据，按照以下区间分为八组
①[0，30），②[30，60）③[60，90）④[90，120）⑤[120，150）⑥[150，180）⑦[180，210）⑧[210，240），得到频率布直方图如图，已知抽取的学生中星期天晚上学习时间少于60分钟的人数为5人．
（1）求n的值并补全下列频率分布直方图；
（2）如果把“学生晚上学习时间达到两小时”作为是否充分利用时间的标准，对抽取的n名学生，完成下列2×2列联表：
利用时间充分利用时间不充分合计
走读生
 
 
 
住校生
 
10
 
合计
 
 
 
据此资料，你是否认为学生“利用时间是否充分”与走读、住校有关？
（3）若在第①组、第②组共抽出2人调查影响有效利用时间的原因，求抽出的2人中第①组第②组各有1人的概率．
已知△ABC的外接圆半径为1，且A+C=2B，若角A，B，C所对的边长分别为a，b，c．
（1）求a2+c2的取值范围；
（2）求△ABC面积的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网