题目内容
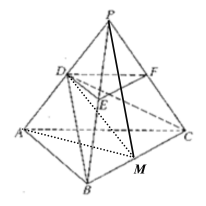
【题目】如图,![]() 是底面边长为1的正三棱锥,
是底面边长为1的正三棱锥,![]() 分别为棱长
分别为棱长![]() 上的点,截面
上的点,截面![]() 底面
底面![]() ,且棱台
,且棱台![]() 与棱锥
与棱锥![]() 的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
的棱长和相等.(棱长和是指多面体中所有棱的长度之和)

(1)证明:![]() 为正四面体;
为正四面体;
(2)若![]() ,求二面角
,求二面角![]() 的大小;(结果用反三角函数值表示)
的大小;(结果用反三角函数值表示)
(3)设棱台![]() 的体积为
的体积为![]() ,是否存在体积为
,是否存在体积为![]() 且各棱长均相等的直平行六面体,使得它与棱台
且各棱长均相等的直平行六面体,使得它与棱台![]() 有相同的棱长和?若存在,请具体构造出这样的一个直平行六面体,并给出证明;若不存在,请说明理由.
有相同的棱长和?若存在,请具体构造出这样的一个直平行六面体,并给出证明;若不存在,请说明理由.
(注:用平行于底的截面截棱锥,该截面与底面之间的部分称为棱台,本题中棱台的体积等于棱锥![]() 的体积减去棱锥
的体积减去棱锥![]() 的体积.)
的体积.)
【答案】(1)证明见解析;(2)![]() ;(3)存在,证明见解析.(注:所构造直平行六面体不唯一,只需题目满足要求即可)
;(3)存在,证明见解析.(注:所构造直平行六面体不唯一,只需题目满足要求即可)
【解析】
(1)根据棱长和相等可知![]() ,根据面面平行关系和棱锥为正三棱锥可证得
,根据面面平行关系和棱锥为正三棱锥可证得![]() ,进而证得
,进而证得![]() 各棱长均相等,由此得到结论;(2)取
各棱长均相等,由此得到结论;(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,根据等腰三角形三线合一的性质和线面垂直判定定理可证得
,根据等腰三角形三线合一的性质和线面垂直判定定理可证得![]() 平面
平面![]() ,由线面垂直性质可知
,由线面垂直性质可知![]() ,从而得到
,从而得到![]() 即为所求二面角的平面角;易知
即为所求二面角的平面角;易知![]() ,从而得到
,从而得到![]() ,在
,在![]() 中根据长度关系可求得
中根据长度关系可求得![]() ,从而得到结果;(3)设直平行六面体的棱长均为
,从而得到结果;(3)设直平行六面体的棱长均为![]() ,底面相邻两边夹角为
,底面相邻两边夹角为![]() ,根据正四面体
,根据正四面体![]() 体积为
体积为![]() ,可验证出
,可验证出![]() ;又所构造六面体体积为
;又所构造六面体体积为![]() ,知
,知![]() ,只需满足
,只需满足![]() 即可满足要求,从而得到结果.
即可满足要求,从而得到结果.
(1)![]() 棱台
棱台![]() 与棱锥
与棱锥![]() 的棱长和相等
的棱长和相等
![]()
![]() 平面
平面![]() 平面
平面![]() ,三棱锥
,三棱锥![]() 为正三棱锥
为正三棱锥
![]()
![]()
![]()
![]() 为正四面体
为正四面体
(2)取![]() 的中点
的中点![]() ,连接
,连接![]()
![]() ,
,![]()
![]() ,
,![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
![]()
![]() 为二面角
为二面角![]() 的平面角
的平面角
由(1)知,![]() 各棱长均为
各棱长均为![]()
![]()
![]() 为
为![]() 中点
中点 ![]()
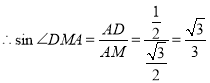
![]()
即二面角![]() 的大小为:
的大小为:![]()
(3)存在满足题意的直平行六面体,理由如下:
棱台![]() 的棱长和为定值
的棱长和为定值![]() ,体积为
,体积为![]()
设直平行六面体的棱长均为![]() ,底面相邻两边夹角为
,底面相邻两边夹角为![]()
则该六面体棱长和为![]() ,体积为
,体积为![]()
![]() 正四面体
正四面体![]() 体积为:
体积为:![]()
![]()
![]()
![]() 时,满足要求
时,满足要求
故可构造棱长均为![]() ,底面相邻两边夹角为
,底面相邻两边夹角为![]() 的直平行六面体即可满足要求
的直平行六面体即可满足要求

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目