题目内容
1.在△ABC中,若$\overrightarrow{AB}$$+\overrightarrow{AC}$=4$\overrightarrow{AP}$,则$\overrightarrow{PB}$=( )| A. | $\frac{3}{4}$$\overrightarrow{AB}$$-\frac{1}{4}$$\overrightarrow{AC}$ | B. | -$\frac{3}{4}$$\overrightarrow{AB}$$+\frac{1}{4}$$\overrightarrow{AC}$ | C. | -$\frac{1}{4}$$\overrightarrow{AB}$$+\frac{3}{4}$$\overrightarrow{AC}$ | D. | $\frac{1}{4}$$\overrightarrow{AB}$$-\frac{3}{4}$$\overrightarrow{AC}$ |
分析 如图所示,以AB,AC为邻边作平行四边形ABEC,设D为BC的中点,$\overrightarrow{AB}$$+\overrightarrow{AC}$=4$\overrightarrow{AP}$,可得$\overrightarrow{AB}$$+\overrightarrow{AC}$=$\overrightarrow{AE}$=2$\overrightarrow{AD}$=4$\overrightarrow{AP}$,$\overrightarrow{AD}$=2$\overrightarrow{AP}$,即点P为AD的中点.再利用向量三角形法则与平行四边形法则即可得出.
解答 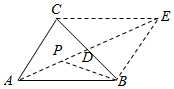 解:如图所示,以AB,AC为邻边作平行四边形ABEC,设D为BC的中点,
解:如图所示,以AB,AC为邻边作平行四边形ABEC,设D为BC的中点,
∵$\overrightarrow{AB}$$+\overrightarrow{AC}$=4$\overrightarrow{AP}$,
∴$\overrightarrow{AB}$$+\overrightarrow{AC}$=$\overrightarrow{AE}$=2$\overrightarrow{AD}$=4$\overrightarrow{AP}$,
∴$\overrightarrow{AD}$=2$\overrightarrow{AP}$,即点P为AD的中点.
则$\overrightarrow{PB}$=-$\frac{1}{2}(\overrightarrow{BA}+\overrightarrow{BD})$=-$\frac{1}{2}$$\overrightarrow{BA}$-$\frac{1}{4}$$\overrightarrow{BC}$=-$\frac{1}{2}$$\overrightarrow{BA}$-$\frac{1}{4}$×$(\overrightarrow{BA}+\overrightarrow{AC})$=$\frac{3}{4}$$\overrightarrow{AB}$-$\frac{1}{4}$$\overrightarrow{AC}$.
故选:A.
点评 本题考查了向量三角形法则与平行四边形法则、向量共线定理,考查了推理能力与计算能力,属于中档题.

| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
| A. | $\frac{4π}{81}$ | B. | $\frac{π}{6}$ | C. | $\frac{4}{81}$ | D. | $\frac{1}{6}$ |
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2}{3}$ |
| A. | 1 | B. | -1 | C. | 3 | D. | 0 |