题目内容
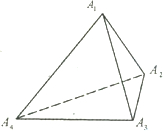 (1)如图,对于任一给定的四面体A1A2A3A4,找出依次排列的四个相互平行的α1,α2,α3,α4,使得Ai∈αi(i=1,2,3,4),且其中每相邻两个平面间的距离都相等;
(1)如图,对于任一给定的四面体A1A2A3A4,找出依次排列的四个相互平行的α1,α2,α3,α4,使得Ai∈αi(i=1,2,3,4),且其中每相邻两个平面间的距离都相等;(2)给定依次排列的四个相互平行的平面α1,α2,α3,α4,其中每相邻两个平面间的距离都为1,若一个正四面体A1A2A3A4 的四个顶点满足:Ai∈αi(i=1,2,3,4),求该正四面体A1A2A3A4的体积.
分析:(1)先取A2A4的三等分点p2,p3,A1A3的中点M,A2A4,的中点N,过三点A2,P2,M,作平面α2,过三点p3,A3,N作平面α3,先得到两个平行平面,再过点A1,A4,分别作平面α1,α4,与平面α3平行即可.
(2)直接利用(1)中的四个平面以及四面体,建立出以△A2A3A4的中心O为坐标原点,以直线A4O为y轴,直线OA1为Z轴的直角坐标系,求出各点对应坐标,求出平面A3P3N的法向量,利用α1,α2,α3,α4相邻平面之间的距离为1求出正四面体的棱长,进而代入体积公式求出体积即可.
(2)直接利用(1)中的四个平面以及四面体,建立出以△A2A3A4的中心O为坐标原点,以直线A4O为y轴,直线OA1为Z轴的直角坐标系,求出各点对应坐标,求出平面A3P3N的法向量,利用α1,α2,α3,α4相邻平面之间的距离为1求出正四面体的棱长,进而代入体积公式求出体积即可.
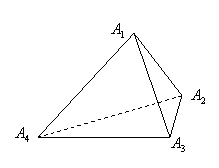
解答: 解:(1)如图所示,取A1A4的三等分点p2,p3,A1A3的中点M,A2A4,的中点N,
解:(1)如图所示,取A1A4的三等分点p2,p3,A1A3的中点M,A2A4,的中点N,
过三点A2,P2,M,作平面α2,过三点A3,P3,N作平面α3,
因为A2P2∥NP3,A3P3∥MP2,所以平面α2∥α3,
再过点A1,A4,分别作平面α1,α4,与平面α3平行,
那么四个平面α1,α2,α3,α4依次互相平行,
由线段A1A4被平行平面α1,α2,α3,α4截得的线段相等知,其
中每相邻两个平面间的距离相等,故α1,α2,α3,α4为所求平面.
(2):当(1)中的四面体为正四面体,若所得的四个平行平面每相邻两平面之间的距离为1,
则正四面体A1A2A3A4就是满足题意的正四面体.
设正四面体的棱长为a,以△A2A3A4的中心O为坐标原点,以直线A4O为y轴,直线OA1为Z轴建立如图所示的右手直角坐标系,
则A1(0,0,
a),A2(-
,
a,0),A3(
,
a,0),A4(0,-
a,0).
令P2,P3为.A1A4的三等分点,N为A2A4的中点,有P3(0,-
a,
a),N(-
,-
a,0),
所以
=(-
,
a,-
a),
=(
a,
a,0),
=(-
,
a,0)
设平面A3P3N的法向量
=(x,y,z),有
即
,
所以
=(1,-
,-
).因为α1,α2,α3,α4相邻平面之间的距离为1,
所以点A4到平面A3P3N 的距离
=1,解得a=
,
由此可得,边长为
的正四面体A1A2A3A4满足条件.
所以所求四面体的体积V=
Sh=
×
a2×
a=
a3=
.
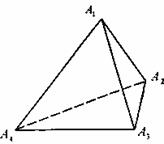
 解:(1)如图所示,取A1A4的三等分点p2,p3,A1A3的中点M,A2A4,的中点N,
解:(1)如图所示,取A1A4的三等分点p2,p3,A1A3的中点M,A2A4,的中点N,过三点A2,P2,M,作平面α2,过三点A3,P3,N作平面α3,
因为A2P2∥NP3,A3P3∥MP2,所以平面α2∥α3,
再过点A1,A4,分别作平面α1,α4,与平面α3平行,
那么四个平面α1,α2,α3,α4依次互相平行,
由线段A1A4被平行平面α1,α2,α3,α4截得的线段相等知,其
中每相邻两个平面间的距离相等,故α1,α2,α3,α4为所求平面.
(2):当(1)中的四面体为正四面体,若所得的四个平行平面每相邻两平面之间的距离为1,
则正四面体A1A2A3A4就是满足题意的正四面体.
设正四面体的棱长为a,以△A2A3A4的中心O为坐标原点,以直线A4O为y轴,直线OA1为Z轴建立如图所示的右手直角坐标系,
则A1(0,0,
| ||
| 3 |
| a |
| 2 |
| ||
| 6 |
| a |
| 2 |
| ||
| 6 |
| ||
| 3 |
令P2,P3为.A1A4的三等分点,N为A2A4的中点,有P3(0,-
2
| ||
| 9 |
| ||
| 9 |
| a |
| 4 |
| ||
| 12 |
所以
| P3N |
| a |
| 4 |
5
| ||
| 36 |
| ||
| 9 |
| NA3 |
| 3 |
| 4 |
| ||
| 4 |
| A4N |
| a |
| 4 |
| ||
| 4 |
设平面A3P3N的法向量
| n |
|
|
所以
| n |
| 3 |
| 6 |
所以点A4到平面A3P3N 的距离
|(-
| ||||||||||
|
| 10 |
由此可得,边长为
| 10 |
所以所求四面体的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| ||
| 3 |
| ||
| 12 |
5
| ||
| 3 |
点评:本题考查平面和平面之间的关系以及四面体的体积公式的应用.是道难题,第一问的关键点在与设出A2A4的三等分点p2,p3,过这二个点先作两个过已知点的平行平面,另两个平面就好求了.

练习册系列答案
相关题目
 ,找出依
,找出依 ,使
,使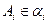 (i=1,2,3,4),且其中每相邻两个平面间
(i=1,2,3,4),且其中每相邻两个平面间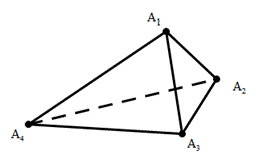
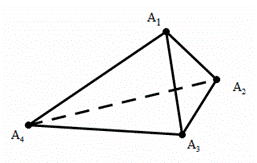
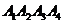 ,找出依
,找出依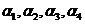 ,使
,使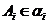 (i=1,2,3,4),且其中每相邻两个平面间
(i=1,2,3,4),且其中每相邻两个平面间