题目内容
4.已知函数f(x)=$\left\{\begin{array}{l}{|lnx|,x>0}\\{{x}^{2}+4x+1,x≤0}\end{array}\right.$,若关于x的方程f2(x)-bf(x)+c=0(b,c∈R)有8个不同的实数根,则由点(b,c)确定的平面区域的面积为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 题中原方程f2(x)-bf(x)+c=0有8个不同实数解,即要求对应于f(x)=某个常数K,有2个不同的K,再根据函数对应法则,每一个常数可以找到4个x与之对应,就出现了8个不同实数解,故先根据题意作出f(x)的简图,由图可知,只有满足条件的K在开区间(0,1)时符合题意.再根据一元二次方程根的分布理论可以得出答案.
解答 解:根据题意作出f(x)的简图: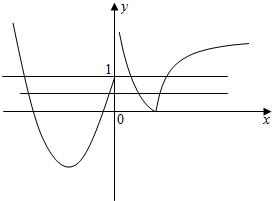
由图象可得当f(x)∈(0,1]时,有四个不同的x与f(x)对应.再结合题中“方程f2(x)-bf(x)+c=0有8个不同实数解”,
可以分解为形如关于k的方程k2-bk+c=0有两个不同的实数根K1、K2,且K1和K2均为大于0且小于等于1的实数.
列式如下:$\left\{\begin{array}{l}{{b}^{2}-4c>0}\\{0<\frac{b}{2}<1}\\{{0}^{2}-b×0+c>0}\\{{1}^{2}-b+c≥0}\end{array}\right.$,化简得$\left\{\begin{array}{l}{c<\frac{{b}^{2}}{4}}\\{1-b+c≥0}\\{c>0}\\{0<b<2}\end{array}\right.$,
此不等式组表示的区域如图: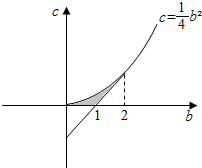
则图中阴影部分的面积即为答案,由定积分的知识得
S=${∫}_{0}^{2}(\frac{1}{4}{b}^{2})db$-$\frac{1}{2}$×1×1=$\frac{1}{6}$
故选:A
点评 本题考查了函数的图象与一元二次方程根的分布的知识,同时考查定积分等知识,较为综合;采用数形结合的方法解决,使本题变得易于理解.

练习册系列答案
相关题目
12.在单调递增的等差数列{an}中,若a3=1,a2a4=$\frac{3}{4}$,则a1=( )
| A. | -1 | B. | 0 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
9.曲线y=$\frac{1-2x}{{x}^{2}}$在点(-1,3)处的切线方程为( )
| A. | y=4x-7 | B. | y=4x+7 | C. | y=-4x-1 | D. | y=-4x+3 |
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左右焦点,上下顶点依次为F1,F2,B1,B2,若四边形F1B1F2B2的面积为8,且椭圆的离心率为$\frac{\sqrt{2}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左右焦点,上下顶点依次为F1,F2,B1,B2,若四边形F1B1F2B2的面积为8,且椭圆的离心率为$\frac{\sqrt{2}}{2}$.