题目内容
在直角坐标中,A(3,1),B(-3,-3),C(l,4),P是 和
和 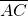 夹角平分线上的一点,且
夹角平分线上的一点,且 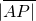 =2,则
=2,则 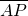 的坐标是
的坐标是
- A.
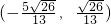
- B.(-
 ,
, )
) - C.
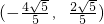
- D.
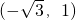
A
分析:由题意可得cos∠BAP=cos∠CAP>0,设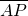 的坐标为(x,y),而由两个向量的夹角公式求得x、y之间的关系,再由|
的坐标为(x,y),而由两个向量的夹角公式求得x、y之间的关系,再由| |=
|= =2,求得x、y的值,即可得到
=2,求得x、y的值,即可得到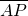 的坐标.
的坐标.
解答:由题意可得 =(-6,-4),
=(-6,-4), =(-2,3),∠BAP=∠CAP,
=(-2,3),∠BAP=∠CAP,
∴cos∠BAP=cos∠CAP>0.
设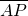 的坐标为(x,y),而由两个向量的夹角公式可得
的坐标为(x,y),而由两个向量的夹角公式可得
cos∠BAP=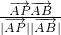 =
=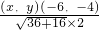 =
=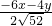 ,
,
cos∠CAP=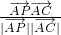 =
=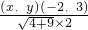 =
=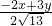 ,
,
∴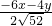 =
=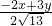 >0,解得 x=-5y<0.
>0,解得 x=-5y<0.
再由| |=
|= =2,可得 x=-5
=2,可得 x=-5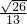 ,y=
,y=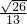 ,故
,故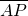 的坐标是
的坐标是 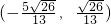 ,
,
故选A.
点评:本题主要考查两个向量的夹角公式,两个向量坐标形式的运算,注意cos∠BAP=cos∠CAP>0,这是解题的易错点,属于中档题.
分析:由题意可得cos∠BAP=cos∠CAP>0,设
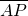 的坐标为(x,y),而由两个向量的夹角公式求得x、y之间的关系,再由|
的坐标为(x,y),而由两个向量的夹角公式求得x、y之间的关系,再由| |=
|= =2,求得x、y的值,即可得到
=2,求得x、y的值,即可得到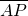 的坐标.
的坐标.解答:由题意可得
 =(-6,-4),
=(-6,-4), =(-2,3),∠BAP=∠CAP,
=(-2,3),∠BAP=∠CAP,∴cos∠BAP=cos∠CAP>0.
设
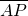 的坐标为(x,y),而由两个向量的夹角公式可得
的坐标为(x,y),而由两个向量的夹角公式可得cos∠BAP=
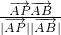 =
=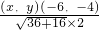 =
=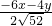 ,
,cos∠CAP=
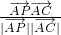 =
=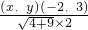 =
=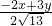 ,
,∴
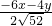 =
=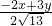 >0,解得 x=-5y<0.
>0,解得 x=-5y<0.再由|
 |=
|= =2,可得 x=-5
=2,可得 x=-5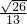 ,y=
,y=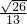 ,故
,故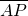 的坐标是
的坐标是 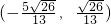 ,
,故选A.
点评:本题主要考查两个向量的夹角公式,两个向量坐标形式的运算,注意cos∠BAP=cos∠CAP>0,这是解题的易错点,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目