Question

已知直线l:y=k(x-a)及圆O：x²+y²=r²(a＞r＞0)，直线l与圆O相交于A、B两点，求当k变动时，弦AB中点的轨迹方程.

Answer 1

解：设轨迹上任一点为M(x,y),A(x₁,y₁)、B(x₂,y₂).

由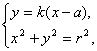得(1+k²)x²-2ak²x+a²k²-r²=0.

设其两根为x₁、x₂,则x=,即x=.                             ①

∵y=k(x-a),                                                                   ②

∴由①②消去k得x²+y²-ax=0.

由Δ=(-2ak²)²-4(1+k²)(a²k²-r²)＞0,

得k²＜,∴x=＜.

∴所求轨迹方程为x²+y²-ax=0(0≤x＜).