题目内容

在数列{a_n}中，a₁=1，3a_na_n-1+a_n-a_n-1=0（n≥2，n∈N^*）．
（1）试判断数列 $数学公式$ 是否成等差数列；
（2）设{b_n}满足b_n= $数学公式$ ，求数列{b_n}的前n项和S_n；
（3）若λa_n+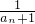 $数学公式$ ≥λ对任意n≥2的整数恒成立，求实数λ的取值范围．

解：（1）∵数列{a_n}中，a₁=1，3a_na_n-1+a_n-a_n-1=0（n≥2，n∈N^*），
∴a_n-1-a_n=3a_na_n-1，
∴ $\text{[math]}$ （n≥2）．
故数列{ $\text{[math]}$ }是等差数列．
（2）由（1）的结论可得b_n= $\text{[math]}$ =1+（n-1）×3，
所以b_n=3n-2，
∴S_n= $\text{[math]}$ = $\text{[math]}$ ．
（3）将a_n= $\text{[math]}$ = $\text{[math]}$ 代入λa_n+ $\text{[math]}$ ≥λ并整理得λ（1- $\text{[math]}$ ）≤3n+1，
∴λ≤ $\text{[math]}$ ，
原命题等价于该式对n≥2恒成立．
设C_n= $\text{[math]}$ ，
则C_n+1-C_n= $\text{[math]}$ ＞0，C_n+1＞C_n，
∵n=2时，C_n的最小值C₂为 $\text{[math]}$ ，
∴λ的取值范围是（-∞， $\text{[math]}$ ]．
分析：（1）由已知可得 $\text{[math]}$ （n≥2）．由此能够证明数列{ $\text{[math]}$ }是等差数列．
（2）由（1）的结论可得b_n= $\text{[math]}$ =1+（n-1）×3，所以b_n=3n-2，由此能求出S_n．
（3）将a_n= $\text{[math]}$ = $\text{[math]}$ 代入λa_n+ $\text{[math]}$ ≥λ，并整理得λ（1- $\text{[math]}$ ）≤3n+1，故λ≤ $\text{[math]}$ ，原命题等价于该式对n≥2恒成立．由此能够求出实数λ的取值范围．
点评：本题考查等差数列的判断、数列前n项和公式的求法和求实数λ的取值范围．综合性强，难度大，有一定的探索性，对数学思维能力要求较高，是高考的重点．解题时要认真审题，仔细解答．