题目内容
求过曲线xy=a2上任一点的切线在x,y轴上的截距之积.
解:由xy=a2得y=![]() a2x,y′=(
a2x,y′=(![]() )′=-
)′=-![]() ,
,
所以曲线xy=a2上任一点M(x0,y0)的切线的斜率为k=-![]() ,
,
切线方程为y-y0=-![]() (x-x0),即y=-
(x-x0),即y=-![]() x+
x+![]() +y0.
+y0.
因为M(x0,y0)在曲线xy=a2上,所以y0=![]() .
.
所以切线方程可写成y=-![]() x+2y0=-
x+2y0=-![]() x+2y0.
x+2y0.
令x=0,解得切线的纵截距为y=2y0,
令y=0,解得切线的横截距为x=2x0,
于是两截距之积为2x0·2y0=4x0y0=4a2.
即曲线xy=a2上任一点的切线在两坐标轴上的两截距之积为4a2.

练习册系列答案
相关题目
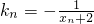 的直线交曲线C于另一点An+1(xn+1,yn+1),点A1,A2,…,An,…的横坐标构成数列{xn},其中
的直线交曲线C于另一点An+1(xn+1,yn+1),点A1,A2,…,An,…的横坐标构成数列{xn},其中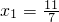 .
.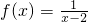 ,an=f(xn),求{an}的通项公式;
,an=f(xn),求{an}的通项公式;