题目内容
若曲线C:xy=1,过C上一点An(xn,yn)作一斜率为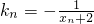 的直线交曲线C于另一点An+1(xn+1,yn+1),点A1,A2,…,An,…的横坐标构成数列{xn},其中
的直线交曲线C于另一点An+1(xn+1,yn+1),点A1,A2,…,An,…的横坐标构成数列{xn},其中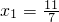 .
.
(1)求xn与xn+1的关系式;
(2)若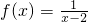 ,an=f(xn),求{an}的通项公式;
,an=f(xn),求{an}的通项公式;
(3)求证:(-1)x1+(-1)2x2+…+(-1)nxn<1(n∈N*).
解:(1)
∴xn+1xn=xn+2(4分)
(2)
∴ (8分)
(8分)
又 ∴
∴ 为等比数列
为等比数列
∴
∴ (10分)
(10分)
(3) ,∴
,∴
当n为奇数时,(-1)nxn+(-1)n+1xn+1
=
= (12分)
(12分)
当n为偶数时,(-1)x1+(-1)2x2++(-1)nxn

 (13分)
(13分)
当n为奇数时,(-1)x1+(-1)2x2++(-1)nxn

=
综上,(-1)x1+(-1)2x2++(-1)nxn<1.(14分)
分析:(1)由题设条件知 ,由此可知xn+1xn=xn+2.
,由此可知xn+1xn=xn+2.
(2)由题意知 ,由此可知
,由此可知 ,所以
,所以 .
.
(3)由题意知 ,由此入手能够推导出(-1)x1+(-1)2x2++(-1)nxn<1.
,由此入手能够推导出(-1)x1+(-1)2x2++(-1)nxn<1.
点评:本题考查数列性质的综合运用,解题时要认真审题,仔细解答.

∴xn+1xn=xn+2(4分)
(2)

∴
 (8分)
(8分)又
 ∴
∴ 为等比数列
为等比数列∴

∴
 (10分)
(10分)(3)
 ,∴
,∴
当n为奇数时,(-1)nxn+(-1)n+1xn+1
=

=
 (12分)
(12分)当n为偶数时,(-1)x1+(-1)2x2++(-1)nxn

 (13分)
(13分)当n为奇数时,(-1)x1+(-1)2x2++(-1)nxn

=

综上,(-1)x1+(-1)2x2++(-1)nxn<1.(14分)
分析:(1)由题设条件知
 ,由此可知xn+1xn=xn+2.
,由此可知xn+1xn=xn+2.(2)由题意知
 ,由此可知
,由此可知 ,所以
,所以 .
.(3)由题意知
 ,由此入手能够推导出(-1)x1+(-1)2x2++(-1)nxn<1.
,由此入手能够推导出(-1)x1+(-1)2x2++(-1)nxn<1.点评:本题考查数列性质的综合运用,解题时要认真审题,仔细解答.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
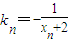 的直线交曲线C于另一点An+1(xn+1,yn+1),点A1,A2,…,An,…的横坐标构成数列{xn},其中
的直线交曲线C于另一点An+1(xn+1,yn+1),点A1,A2,…,An,…的横坐标构成数列{xn},其中 .
.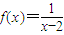 ,an=f(xn),求{an}的通项公式;
,an=f(xn),求{an}的通项公式;