题目内容
证明下面两个命题:
(1)在所有周长相等的矩形中,只有正方形的面积最大;
(2)余弦定理:如右图,在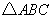 中,
中,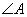 、
、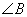 、
、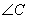 所对的边分别为
所对的边分别为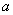 、
、 、
、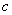 ,则
,则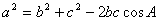 .
.
证明一:(1)设长方形的长,宽分别为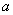 ,
, ,由题设
,由题设 为常数
为常数
由基本不等式2:
 ,可得:
,可得: ,
,
当且仅当 时,等号成立,
时,等号成立,
即当且仅当长方形为正方形时,面积 取得最大值
取得最大值 .
.
证明二:(1)设长方形的周长为 ,长为
,长为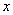 ,则宽为
,则宽为
于是,长方形的面积 ,
,
所以,当且仅当 时,面积最大为
时,面积最大为 ,此时,长方形的为
,此时,长方形的为 ,即为正方形
,即为正方形
(2)证法一:




 .
.
故, .
.
证法二 已知 中
中 所对边分别为
所对边分别为 以
以 为原点,
为原点,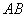 所在直线为
所在直线为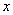 轴建立直角坐标系,则
轴建立直角坐标系,则 ,
,

 .
.
故, .
.
证法三 过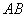 边上的高
边上的高 ,则
,则

 .
.
故, .
.

练习册系列答案
相关题目
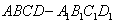 的棱上到异面直线
的棱上到异面直线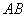 ,
,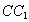 的距离相等的点的个数为( )
的距离相等的点的个数为( )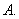 2
2 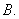 3
3 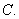 4
4 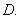 5
5 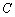 的方程为
的方程为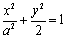
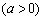 ,其焦点在
,其焦点在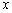 轴上,点
轴上,点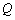
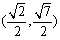 为椭圆上一点.
为椭圆上一点.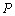
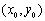 满足
满足 ,其中
,其中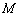 、
、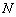 是椭圆
是椭圆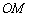 与
与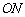
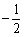 ,求证:
,求证: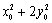 为定值;
为定值;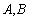 ,使得
,使得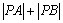 为定值?
为定值?  在区间
在区间 上存在一个零点,则实数
上存在一个零点,则实数







 为奇函数,
为奇函数, 分别为函数图像上相邻的最高点与最低点,且
分别为函数图像上相邻的最高点与最低点,且 ,则该函数的一条对称轴为( ).
,则该函数的一条对称轴为( ).  .
.

 .
. 
 .
.
 的定义域是_____________.
的定义域是_____________. 的顶点坐标分别为
的顶点坐标分别为 ,
, ,点
,点 在直线
在直线 上运动,
上运动, 为坐标原点,
为坐标原点, 为△
为△ 的最小值为__________.
的最小值为__________. 的底面边长为
的底面边长为 ,侧棱长为
,侧棱长为 ,
, 为棱
为棱 的中点.
的中点. 与
与 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示); .
.
 C.
C. 弧度 D.10弧度
弧度 D.10弧度