题目内容
|
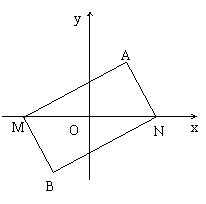如图：平行四边形
的周长为8，点
的坐标分别为
．
（Ⅰ）求点
所在的曲线方程；
（Ⅱ）过点
的直线
与(Ⅰ)中曲线交于点
，与Y 轴交于点
，且//
，求证：
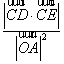为定值．
解：（Ⅰ）因为四边形
是平行四边形,周长为8,所以两点
到
的距离之和均为4,可知所求曲线为椭圆 …………1分
由椭圆定义可知，
，
所求曲线方程为
…4分
（Ⅱ）由已知可知直线
的斜率存在，又直线过点
设直线的方程为：
………5分
代入曲线方程
，并整理得
点在曲线上,所以
(
,
) ……8分
,
,
………………9分
因为
//,所以设的方程为
………10分
代入曲线方程，并整理得
所以
……………11分
所以： 
为定值 …12分
练习册系列答案
相关题目
已知x与y之间的一组数据如表，则y与x的线性回归方程
=
x+
必过点 ．
| ? |
| y |
| ? |
| b |
| ? |
| a |
| x | 0 | 1 | 2 | 3 |
| y | 2 | 4 | 6 | 8 |
{2.4.6.8.10.12}，则集合P=