题目内容
方程
=
的解n=（ ）
| 1+3+5+…+(2n+1) |
| 2+4+6+…+2n |
| 116 |
| 115 |
分析：代入求和公式可得关于n的方程，解之可得．
解答：解：由等差数列的求和公式可得
=
=
=
，解之可得n=115，
故选B
| 1+3+5+…+(2n+1) |
| 2+4+6+…+2n |
=
| ||
|
| n+1 |
| n |
| 116 |
| 115 |
故选B
点评：本题考查等差数列的求和公式，涉及方程的解法，属基础题．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
下列算法输出的结果是 （ ）
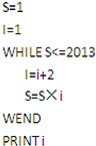如图算法输出的结果是（ ）| A、满足1×3×5×…×n＞2013的最小整数n | B、1+3+5+…+2013 | C、求方程1×3×5×…×n=2013中的n值 | D、1×3×5×…×2013 |
，若方程
无实数解，则方程
的实数根的个数为