题目内容
【题目】如图,![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是
是![]() 的中点,点
的中点,点![]() 沿着路径
沿着路径![]() 在正方形边上运动所经过的路程为
在正方形边上运动所经过的路程为![]() ,
,![]() 的面积为
的面积为![]() .
.

(1)求![]() 的解析式及定义域;
的解析式及定义域;
(2)求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 位置.
位置.
【答案】(1)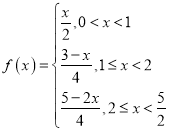 ,函数
,函数![]() 的定义域为
的定义域为![]() ;
;
(2)![]() 面积的最大值为
面积的最大值为![]() ,此时点
,此时点![]() 与点
与点![]() 重合.
重合.
【解析】
(1)分点![]() 在线段
在线段![]() (不包括点
(不包括点![]() 、
、![]() )、
)、![]() (不包括点
(不包括点![]() )、
)、![]() (不包括点
(不包括点![]() ),即对
),即对![]() 分
分![]() 、
、![]() 、
、![]() 三种情况讨论,计算出
三种情况讨论,计算出![]() 关于
关于![]() 的表达式,即可得出函数
的表达式,即可得出函数![]() 的解析式,并求出该函数的定义域;
的解析式,并求出该函数的定义域;
(2)分段求出函数![]() 的每支函数的最大值,比较大小后得出函数
的每支函数的最大值,比较大小后得出函数![]() 的最大值,并求出对应的
的最大值,并求出对应的![]() 的值,即可得出对应的点
的值,即可得出对应的点![]() 的位置.
的位置.
(1)①当点![]() 在线段
在线段![]() (不包括点
(不包括点![]() )时,
)时,![]() ,则
,则![]() ,
,![]() 的高为
的高为![]() ,
,
此时,![]() ;
;
②当点![]() 在线段
在线段![]() (不包括点
(不包括点![]() )时,
)时,![]() ,
,![]() ,
,
![]() 的面积为
的面积为![]() ,
,
![]() 的面积为
的面积为![]() ,
,
直角梯形![]() 的面积为
的面积为![]() ,
,
此时,![]() 的面积
的面积![]() ;
;
③当点![]() 在线段
在线段![]() (不包括点
(不包括点![]() )时,
)时,![]() ,
,![]() 的高为
的高为![]() ,
,
此时,![]() .
.
综上所述,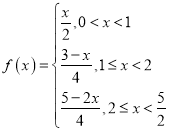 ,函数
,函数![]() 的定义域为
的定义域为![]() ;
;
(2)当![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 单调递增,则
单调递增,则![]() ;
;
当![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 单调递减,则
单调递减,则![]() ;
;
当![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 单调递减,则
单调递减,则![]() .
.
综上所述,当![]() 时,函数
时,函数![]() 取得最大值,即
取得最大值,即![]() .
.
因此,当点![]() 与点
与点![]() 重合时,
重合时,![]() 的面积取到最大值
的面积取到最大值![]() .
.

练习册系列答案
相关题目
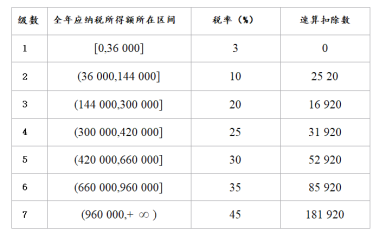
【题目】某工厂生产甲、乙两种产品所得的利润分别为![]() 和
和![]() (万元),事先根据相关资料得出它们与投入资金
(万元),事先根据相关资料得出它们与投入资金![]() (万元)的数据分别如下表和图所示:其中已知甲的利润模型为
(万元)的数据分别如下表和图所示:其中已知甲的利润模型为![]() ,乙的利润模型为
,乙的利润模型为![]() .(
.(![]() 为参数,且
为参数,且![]() ).
).
|
|
|
|
|
|
|
|
|
|
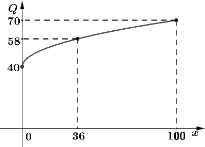
(1)请根据下表与图中数据,分别求出甲、乙两种产品所得的利润与投入资金![]() (万元)的函数模型
(万元)的函数模型
(2)今将![]() 万资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投入资金都不低于
万资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投入资金都不低于![]() 万元.设对乙种产品投入资金
万元.设对乙种产品投入资金![]() (万元),并设总利润为
(万元),并设总利润为![]() (万元),如何分配投入资金,才能使总利润最大?并求出最大总利润.
(万元),如何分配投入资金,才能使总利润最大?并求出最大总利润.