题目内容
已知函数 (1)求![]() 的极大值与极小值;
的极大值与极小值;
(2)设(1)问中函数取得极大值的点为P(x,y),求P所在的曲线.
解析:
(1)∵![]() =16x3-20ax2+8a2x-a3(a≠0),?
=16x3-20ax2+8a2x-a3(a≠0),?
∴f′(x)=48x2-40ax+8a2=8(2x-a)(3x-a).?
由f′(x)=0![]() x=
x=![]() ,x=
,x=![]() ,?
,?
①当a>0时,![]() <
<![]() .
.
x | (-∞, |
| ( |
| ( |
| + | 0 | - | 0 | + |
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
∴当x=![]() 时,f(
时,f(![]() )极大值=
)极大值=![]() ;?
;?
当x=![]() 时,f(
时,f(![]() )极小值=0.?
)极小值=0.?
②当a<0时,
x | (-∞, |
| ( |
| ( |
| + | 0 | - | 0 | + |
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
当x=![]() 时,
时,![]() 取极大值f(
取极大值f(![]() )=0;?
)=0;?
当x=![]() 时,
时,![]() 取得极小值f(
取得极小值f(![]() )=
)=![]() .?
.?
(2)当a>0时,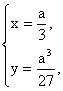 消去a得y=x3(x>0);?
消去a得y=x3(x>0);?
当a<0时,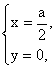 消去a得y=0(x<0).?
消去a得y=0(x<0).?
∴P点的轨迹方程为y=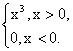 ?
?

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目