题目内容
已知数列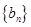 是首项为1,公差为2的等差数列,数列
是首项为1,公差为2的等差数列,数列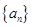 的前n项和
的前n项和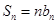 .
.
(I)求数列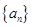 的通项公式;
的通项公式;
(II)设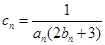 , 求数列
, 求数列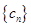 的前n项和
的前n项和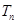 .
.
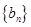 是首项为1,公差为2的等差数列,数列
是首项为1,公差为2的等差数列,数列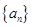 的前n项和
的前n项和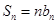 .
.(I)求数列
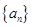 的通项公式;
的通项公式;(II)设
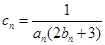 , 求数列
, 求数列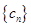 的前n项和
的前n项和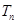 .
.(Ⅰ)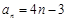 .(Ⅱ)由(Ⅰ)
.(Ⅱ)由(Ⅰ)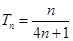 .
.
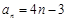 .(Ⅱ)由(Ⅰ)
.(Ⅱ)由(Ⅰ)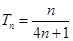 .
. 试题分析:(Ⅰ)根据
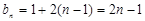 .得到
.得到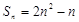 .
.从而通过确定
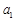 ,当
,当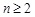 时,
时,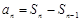 ,验证
,验证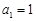 也适合上式,得到所求通项公式.
也适合上式,得到所求通项公式.(Ⅱ)利用“裂项相消法”求和.难度不大,对基础知识的考查较为全面.
试题解析:(Ⅰ)由已知,
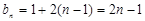 . 2分
. 2分所以
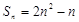 .从而
.从而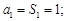
当
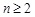 时,
时,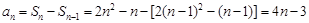 ,
,又
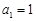 也适合上式,所以
也适合上式,所以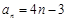 . 6分
. 6分(Ⅱ)由(Ⅰ)
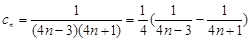 , 8分
, 8分所以
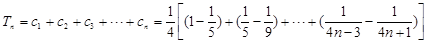
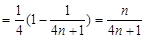 . 12分
. 12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的前n项和为
的前n项和为 ,
,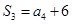 ,且
,且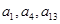 成等比数列.
成等比数列.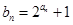 ,求数列
,求数列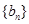 的前n项和.
的前n项和.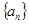 的前
的前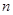 项和为
项和为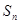 ,且
,且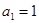 ,
,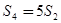 ,数列
,数列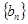 的前
的前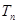 ,满足
,满足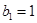 ,
,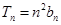 ,
,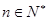 .
.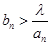 对所有的
对所有的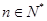 均成立,求实数
均成立,求实数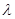 的取值范围.
的取值范围.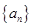 的前
的前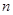 项和为
项和为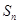 ,且
,且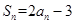
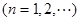 .
.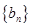 满足
满足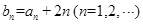 ,求数列
,求数列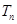 .
.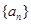 的集合:①对任意
的集合:①对任意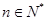 ,
,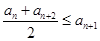 恒成立;②对任意
恒成立;②对任意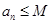 恒成立.
恒成立.
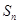 是其前n项和,且
是其前n项和,且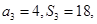 试探究数列
试探究数列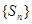 与集合W之间的关系;
与集合W之间的关系;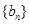 的通项公式为
的通项公式为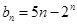 ,且
,且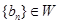 ,求M的取值范围.
,求M的取值范围.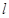 的方程为
的方程为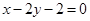 ,数列
,数列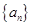 满足
满足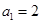 ,其前
,其前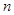 项和为
项和为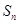 ,点
,点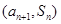 在直线
在直线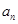 和
和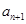 之间插入
之间插入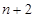 个数组成公差为
个数组成公差为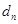 的等差数列,令
的等差数列,令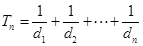 ,试证明
,试证明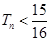 .
.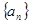 中,中若
中,中若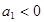 ,
,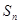 为前
为前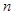 项之和,且
项之和,且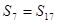 ,则
,则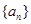 的各项都是正数,且
的各项都是正数,且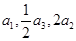 成等差数列,
成等差数列,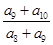 =
=  中,
中,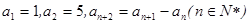 ,则
,则 .
.