题目内容
设集合W是满足下列两个条件的无穷数列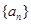 的集合:①对任意
的集合:①对任意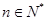 ,
,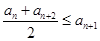 恒成立;②对任意
恒成立;②对任意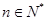 ,存在与n无关的常数M,使
,存在与n无关的常数M,使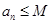 恒成立.
恒成立.
(1)若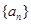 是等差数列,
是等差数列,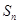 是其前n项和,且
是其前n项和,且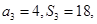 试探究数列
试探究数列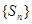 与集合W之间的关系;
与集合W之间的关系;
(2)设数列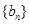 的通项公式为
的通项公式为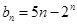 ,且
,且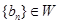 ,求M的取值范围.
,求M的取值范围.
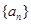 的集合:①对任意
的集合:①对任意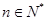 ,
,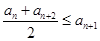 恒成立;②对任意
恒成立;②对任意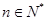 ,存在与n无关的常数M,使
,存在与n无关的常数M,使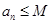 恒成立.
恒成立.
(1)若
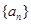 是等差数列,
是等差数列,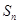 是其前n项和,且
是其前n项和,且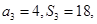 试探究数列
试探究数列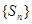 与集合W之间的关系;
与集合W之间的关系;(2)设数列
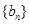 的通项公式为
的通项公式为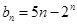 ,且
,且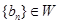 ,求M的取值范围.
,求M的取值范围.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)先根据条件,利用等差数列的性质得到
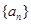 的前n项和
的前n项和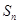 ,然后检验其是否满足①②条件即可;(2)由数列
,然后检验其是否满足①②条件即可;(2)由数列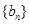 的通项公式经作差可知,当
的通项公式经作差可知,当 时,
时, ,此时,数列
,此时,数列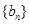 单调递减,当
单调递减,当 时,
时, ,即
,即 ,从而得到数列
,从而得到数列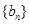 中的最大项为
中的最大项为 ,由
,由 恒成立,从而知
恒成立,从而知 的取值范围是
的取值范围是 .
.试题解析:(1)设等差数列
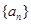 的公差是
的公差是 ,则
,则 解得
解得 1分
1分∴
 (3分)
(3分)∴

∴
 ,适合条件①
,适合条件①又
 ,
,∴当
 或
或 时,
时,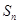 取得最大值20,即
取得最大值20,即 ,适合条件②.
,适合条件②.综上,
 (6分)
(6分)(2)∵
 ,
,∴当
 时,
时, ,此时,数列
,此时,数列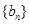 单调递减; 9分
单调递减; 9分当
 时,
时, ,即
,即 , 10分
, 10分因此,数列
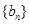 中的最大项是
中的最大项是 , 11分
, 11分∴
 ,即M的取值范围是
,即M的取值范围是 . 12分
. 12分
练习册系列答案
相关题目
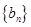 是首项为1,公差为2的等差数列,数列
是首项为1,公差为2的等差数列,数列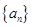 的前n项和
的前n项和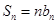 .
.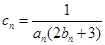 , 求数列
, 求数列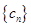 的前n项和
的前n项和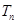 .
.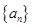 的前
的前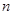 项和为
项和为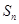 ,且
,且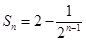 .
.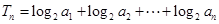 ,求证:
,求证: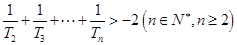 .
.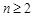 时,其前n项和满足
时,其前n项和满足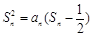 .
.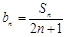 ,数列{bn}的前n项和为
,数列{bn}的前n项和为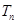 ,求
,求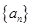 中,
中,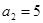 ,
,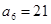 ,记数列
,记数列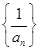 的前
的前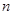 项和为
项和为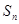 ,
, ;
;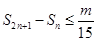 对
对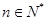 恒成立,则正整数
恒成立,则正整数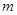 的最小值为 .
的最小值为 . 中,
中, ,则它的前9项和
,则它的前9项和 ( )
( ) 的前
的前 项和为
项和为 ,若
,若 ,则
,则 的值是 .
的值是 .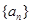 中,
中,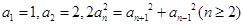 ,则
,则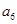 等于( )
等于( )