题目内容
9．已知函数f（x）=-x2+2x+3，x∈[$\frac{1}{2}$，4），则该函数的值域是（-5，4]．分析 配方得f（x）=-（x-1）2+4≤4，可以看出$f（4）＜f（\frac{1}{2}）$，f（4）=-5，从而便可得到-5＜f（x）≤4，这便得出了该函数的值域．
解答 解：f（x）=-（x-1）2+4；
∴f（1）=4是f（x）的最大值，f（4）$＜f（\frac{1}{2}）$，f（4）=-5；
∴-5＜f（x）≤4；
∴该函数的值域为（-5，4]．
故答案为：（-5，4]．
点评 考查函数值域的概念，配方求二次函数值域的方法，要熟悉二次函数的图象．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
4．集合{x|x≥2}表示成区间是（ ）
| A． | （2，+∞） | B． | [2，+∞） | C． | （-∞，2） | D． | （-∞，2] |
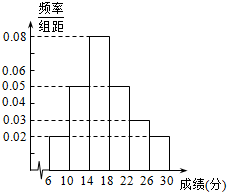为了解某省去年高三考生英语听力成绩，现从某校高三年级随机抽取50名考生的成绩，发现全部介于[6，30]之间，将成绩按如下方式分成6组：第1组[6，10），第2组[10，14），…，第6组[26，30]，如图是按上述分组方法得到的频率分布直方图．
某楼盘开展套餐促销优惠活动，优惠方案如下：选择套餐一的客户可获得优惠2万元，选择套餐二的客户可获得优惠5万元，选择套餐三的客户可获得优惠3万元．根据以往的统计结果绘出参与活动的统计图如图所示，现将频率视为概率．