题目内容

18．某学校一天共排7节课（其中上午4节、下午3节），某教师某天高三年级1班和2班各有一节课，但他要求不能连排2节课（其中上午第4节和下午第1节不算连排），那么该教师这一天的课的所有可能的排法种数共有（　　）
A．16B．15C．32D．30

分析 直接分类讨论得以解决．

解答 解：该教师一个班上第1节课，则另一个班有5种情况，考虑顺序，有10种方法；
一个班上第2节课，则另一个班有4种情况，考虑顺序，有8种方法；
一个班上第3节课，则另一个班有3种情况，考虑顺序，有6种方法；
一个班上第4节课，则另一个班有3种情况，考虑顺序，有6种方法；
一个班上第5节课，则另一个班有7种情况，考虑顺序，有2种方法；
共有10+8+6+6+2=32种方法．
故选：C．

点评 本题考查了排列组合问题，考查分类讨论的数学思想，属于基础题．

练习册系列答案
相关题目
8．已知数列{an}满足a1+2a2+3a3+…+nan=n（n∈N*）．
（1）求数列{an}的通项公式an；
（2）令${b_n}•{2^{\frac{1}{a_n}}}=\frac{1}{{{a_{2n-1}}}}（n∈N*），{T_n}={b_1}+{b_2}+…+{b_n}$，写出Tn关于n的表达式，并求满足Tn＞$\frac{5}{2}$时n的取值范围．
9．已知集合A={x|-3＜x＜6}，B={x|2＜x＜7}，则A∩（∁RB）=（　　）
A．（2，6）B．（2，7）C．（-3，2]D．（-3，2）
6．设集合A={x|0＜x＜2}，B={x|x2+x-2≥0}，则A∩B=（　　）
A．（0，1]B．[1，2）C．[-2，2）D．（0，2）
13．已知函数f（x）为奇函数，且当x＞0时，f（x）=$\sqrt{x}$-$\frac{2}{x}$，则f（-4）=-$\frac{3}{2}$．
3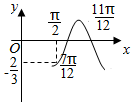．已知函数f（x）=Acos（ωx+φ）的图象如图所示，则f（$\frac{5π}{6}$）=（　　）
A．-$\frac{2}{3}$B．-$\frac{1}{2}$C．$\frac{1}{2}$D．$\frac{2}{3}$
10．公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了“割圆术”．利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”．如图是利用刘徽的“割圆术”思想设计的一个程序框图则输出的值为（　　）
（参考数据：sin15°≈0.2588，sin7.5°≈0.1305）
A．6B．12C．24D．48
7．设函数f（x）=$\frac{2+|x|}{1+|x|}$，则使得f（2x）＞f（x-3）成立的x的取值范围是（　　）
A．（-3，1）B．（-∞，-3）∪（1，+∞）C．（-3，+∞）D．（-∞，1）
8．焦点为（6，0）且与双曲线$\frac{x^2}{2}$-y2=1有相同渐近线的双曲线的方程为（　　）
A．$\frac{{x}^{2}}{24}$-$\frac{{y}^{2}}{12}$=1B．$\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{24}$=1C．$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1D．$\frac{{y}^{2}}{24}$-$\frac{{x}^{2}}{12}$=1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网