题目内容
下列说法正确的个数是( )
①命题“?x∈R,x3-x2+1≤0”的否定是“?x0∈R,x03-x02+1>0”;
②“b=
”是“三个数a,b,c成等比数列”的充要条件;
⑨“m=-1”是“直线mx+(2m-1)y+1=0和直线3x+my+2=0垂直”的充要条件:
④“复数Z=a+bi(a,b∈R)是纯虚数的充要条件是a=0”是真命题.
①命题“?x∈R,x3-x2+1≤0”的否定是“?x0∈R,x03-x02+1>0”;
②“b=
| ac |
⑨“m=-1”是“直线mx+(2m-1)y+1=0和直线3x+my+2=0垂直”的充要条件:
④“复数Z=a+bi(a,b∈R)是纯虚数的充要条件是a=0”是真命题.
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:①利用命题的否定即可判断出.
②“b=±
”是“三个数a,b,c成等比数列”的充要条件,即可判断出;
⑨对m分类讨论:m=0,
与当m≠0,
时,即可判断出;
④“复数Z=a+bi(a,b∈R)是纯虚数的充要条件是a=0,b≠0”,即可判断出.
②“b=±
| ac |
⑨对m分类讨论:m=0,
| 1 |
| 2 |
| 1 |
| 2 |
④“复数Z=a+bi(a,b∈R)是纯虚数的充要条件是a=0,b≠0”,即可判断出.
解答:
解:①命题“?x∈R,x3-x2+1≤0”的否定是“?x0∈R,x03-x02+1>0”,正确;
②“b=±
”是“三个数a,b,c成等比数列”的充要条件,因此②不正确;
⑨直线mx+(2m-1)y+1=0和直线3x+my+2=0.当m=0时,两条直线分别化为-y+1=0,3x+2=0,此时两条直线垂直;
当m=
时,两条直线分别化为
x+1=0,3x+
y+2=0,此时两条直线不垂直;
当m≠0,
时,两条直线的斜率分别为:
,-
,若两条直线垂直,则
•(-
)=-1,解得m=-1;
∴“m=-1”是“直线mx+(2m-1)y+1=0和直线3x+my+2=0垂直”的充分不必要条件,不正确:
④“复数Z=a+bi(a,b∈R)是纯虚数的充要条件是a=0,b≠0”,因此是假命题.
综上可得:只有①是真命题.
故选:A.
②“b=±
| ac |
⑨直线mx+(2m-1)y+1=0和直线3x+my+2=0.当m=0时,两条直线分别化为-y+1=0,3x+2=0,此时两条直线垂直;
当m=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当m≠0,
| 1 |
| 2 |
| -m |
| 2m-1 |
| 3 |
| m |
| -m |
| 2m-1 |
| 3 |
| m |
∴“m=-1”是“直线mx+(2m-1)y+1=0和直线3x+my+2=0垂直”的充分不必要条件,不正确:
④“复数Z=a+bi(a,b∈R)是纯虚数的充要条件是a=0,b≠0”,因此是假命题.
综上可得:只有①是真命题.
故选:A.
点评:本题考查了简易逻辑的有关知识、相互垂直的直线与斜率之间的关系、分类讨论的思想方法、复数为纯虚数的充要条件,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
若实数x,y满足不等式
,且目标函数z=x-2y的最大值为( )
|
| A、1 | B、2 | C、3 | D、4 |
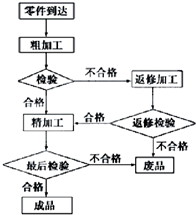 某工厂加工某种零件有三道工序:粗加工,返修加工和精加工.上面是这个零件加工过程的流程图.已知这个零件最后成了废品,则最多经过了
某工厂加工某种零件有三道工序:粗加工,返修加工和精加工.上面是这个零件加工过程的流程图.已知这个零件最后成了废品,则最多经过了