题目内容
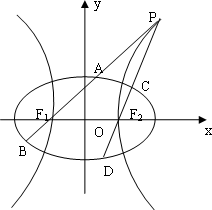
如图，以椭圆
＋
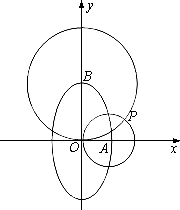
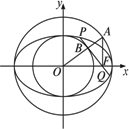
＝1(a＞b＞0)的中心O为圆心，分别以a和b为半径作大圆和小圆．过椭圆右焦点F(c，0)(c＞b)作垂直于x轴的直线交大圆于第一象限内的点A．连结OA交小圆于点B．设直线BF是小圆的切线．
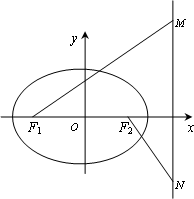
(1)证明c2＝ab，并求直线BF与y轴的交点M的坐标；
(2)设直线BF交椭圆于P、Q两点，证明
·
＝
b2．
答案：
解析：
解析：
|
证明：(1)由题设条件，知Rt△OFA∽△Rt△OBF， 故 因此，c2＝ab． 在Rt△OFA中，FA＝ 于是，直线OA的斜率kOA＝ 设直线BF的斜率为k，则k＝ 这时，直线BF与y轴的交点为M(0，a)． (2)由(1)，得直线BF的方程为y＝kx＋a，且k2＝ 由已知，设P(x1，y1)、Q(x2，y2)，则它们的坐标满足方程组 由方程组③消去y，并整理，得(b2＋a2k2)x2＋2a3kx＋a4－a2b2＝0，④ 由式②、③和④，x1x2＝ 由方程组③消去x，并整理，得(b2＋a2k2)y2＋2ab2y＋a2b2－a2b2k2＝0，⑤ 由式②和⑤，y1y2＝ 综上，得到 注意到a2－ab＋b2＝a2－c2＋b2＝2b2，得 ＝ ＝ ＝ 解析：本小题主要考查椭圆的标准方程的几何性质、直线方程，平面向量、曲线和方程的关系等解析几何的基础知识和基本思想方法，考查推理及运算能力． |
，即
．
＝
＝b．
．
．
．②
③
＝
＝
，
＝
＝
．
·
＝x1x2＋y1y2＝
＋
＝
．
＝
＝
(a2－ab)
练习册系列答案
名校课堂系列答案
相关题目
＋
＝1(a＞b＞0)的离心率为
，以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为4(
＋1)．一等轴双曲线的顶点是该椭圆的焦点，设P为该双曲线上异于顶点的任一点，直线PF1和PF2与椭圆的焦点分别为A、B和C、D．
＝1(a＞b＞0)的右顶点与上顶点分别为A、B，以A为圆心，OA为半径的圆与以B为圆心，OB为半径的圆相交于点O、P．
x2＋1，与坐标轴的交点分别是P、F1、F2，
，求直线l的方程．
＋
＝1(a＞b＞0)过点P(1，
)，其左、右焦点分别为F1，F2，离心率e＝
，M，N是椭圆右准线上的两个动点，且
＝0