题目内容
△ABC中,AC=3,三个内角A,B,C成等差数列.
(1)若cosC=
,求AB;
(2)求
•
的最大值.
(1)若cosC=
| ||
| 3 |
(2)求
| BA |
| BC |
分析:(1)由A,B,C成等差数列易得B=
,进而可得sinC=
,由正弦定理可得答案;(2)由余弦定理可得32=a2+c2-ac,结合基本不等式可得结论.
| π |
| 3 |
| ||
| 3 |
解答:解:(1)∵A,B,C成等差数列,∴2B=A+C,
又A+B+C=π,∴B=
,(2分)
又cosC=
,∴sinC=
,(4分)
由正弦定理得:
=
,
所以AB=
×sinC=
×
=2;(7分)
(2)设角A,B,C的对边为a,b,c,由余弦定理得:b2=a2+c2-2accosB,
即32=a2+c2-ac,(9分)
又a2+c2≥2ac,当且仅当a=c时取到等号,
所以9=a2+c2-ac≥ac(11分)
所以
•
=
ac≤
,
所以
•
的最大值是
.(14分)
又A+B+C=π,∴B=
| π |
| 3 |
又cosC=
| ||
| 3 |
| ||
| 3 |
由正弦定理得:
| AB |
| sinC |
| BC |
| sinA |
所以AB=
| BC |
| sinA |
| 3 | ||||
|
| ||
| 3 |
(2)设角A,B,C的对边为a,b,c,由余弦定理得:b2=a2+c2-2accosB,
即32=a2+c2-ac,(9分)
又a2+c2≥2ac,当且仅当a=c时取到等号,
所以9=a2+c2-ac≥ac(11分)
所以
| BA |
| BC |
| 1 |
| 2 |
| 9 |
| 2 |
所以
| BA |
| BC |
| 9 |
| 2 |
点评:本题为三角形与基本不等式的结合,涉及等差数列的定义和向量的数量积,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
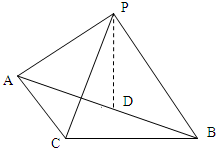 △ABC中,AC=3,BC=4,AB=5.P在平面ABC的射影为AB的中点D.
△ABC中,AC=3,BC=4,AB=5.P在平面ABC的射影为AB的中点D. 如图,在△ABC中,AC=3,AB=5,∠A=120°;
如图,在△ABC中,AC=3,AB=5,∠A=120°;