题目内容
6．
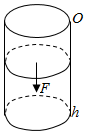如图，在某一温度下，直径为0.2m，高为0.8m上端为活塞的圆柱体内某气体的压强p（N/m2）与体积V（m3）的函数关系式为p=$\frac{80}{V}$，而正压力F（N）与压强p（N/m2）的函数关系为F=pS，其中S（m2）为受力面积．设温度保持不变，要使气体的体积缩小为原来的一半．求活塞克服气体压力做多少功？
分析 设活塞运动的距离为xm，由题意可知W=${∫}_{0}^{0.4}$F（x）dx，根据定积分的计算法则计算即可．
解答 解：设活塞运动的距离为xm，则活塞受到的压强为p=$\frac{80}{V}$，
从而活塞受到的压力为F=pS=$\frac{80}{v}$•S=$\frac{80}{0.8-x}$，
活塞克服气体压力所做的功为：W=${∫}_{0}^{0.4}$F（x）dx=-80ln（0.8-x）|${\;}_{0}^{0.4}$=80ln2，
故活塞克服气体压力做功为80ln2J
点评 本题考查了定积分在物理中的应用，属于中档题．
练习册系列答案
相关题目
19．等差数列{an}的前n项和为Sn，若S2n-1=（2n-1）（2n+1），则Sn=（ ）
| A． | n（n+2） | B． | $\frac{n}{2}$（2n+3） | C． | n（2n+3） | D． | $\frac{n}{2}$（2n+1） |
1．
已知三棱锥的三视图如图所示，其中侧视图是边长为$\sqrt{3}$的正三角形，则该几何体的外接球的体积为（ ）
已知三棱锥的三视图如图所示，其中侧视图是边长为$\sqrt{3}$的正三角形，则该几何体的外接球的体积为（ ）| A． | $\frac{16π}{3}$ | B． | $\frac{32}{3}π$ | C． | 4$\sqrt{3}$π | D． | 16π |
18．
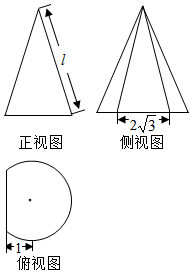如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图，其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$，则圆锥的母线长为（ ）
如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图，其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$，则圆锥的母线长为（ ）| A． | $2\sqrt{2}$ | B． | $2\sqrt{3}$ | C． | 4 | D． | $\sqrt{2}+\sqrt{3}$ |