题目内容
在矩形ABCD中，AB=2，BC=1，取AB中点E，CD中点F，若沿EF将矩形AEFD折起，使得平面AEF⊥平面EFB，则AE中点Q到平面BFD的距离为________．
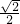
分析：取BF中点O，连接EO，则可得AE中点Q到平面BFD的距离等于E到平面BFD的距离，即EO，由此可得结论．
解答：
解：取BF中点O，连接EO，则EO⊥BF∵平面AEF⊥平面EFB，平面AEF∩平面EFB=EF，DF⊥EF
∴DF⊥平面EFB
∵EO?平面EFB
∴DF⊥EO
∵DF∩BF=F
∴EO⊥平面BFD
∵AE∥DF，AE?平面BFD，DF?平面BFD
∴AE∥平面BFD
∴AE中点Q到平面BFD的距离等于E到平面BFD的距离，即EO
由题意，EFCB是正方形，∴EO=
即AE中点Q到平面BFD的距离等于
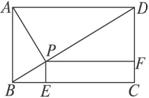
故答案为：
点评：本题考查点到面的结论，考查面面垂直，线面平行，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
如图，在矩形ABCD中，AB=3
如图，在矩形ABCD中，已知AD=2，AB=a（a＞2），E、F、G、H分别是边AD、AB、BC、CD上的点，若AE=AF=CG=CH，问AE取何值时，四边形EFGH的面积最大？并求最大的面积．
的取值范围．
|=
.设
=a, 
=b, 
=c,求|a+b+c|.