题目内容
(本题18分,第(1)小题4分;第(2)小题6分;第(3)小题8分)
如图,已知椭圆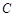 :
: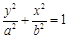
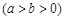 过点
过点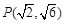 ,上、下焦点分别为
,上、下焦点分别为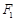 、
、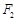 ,
,
向量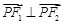 .直线
.直线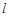 与椭圆交于
与椭圆交于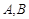 两点,线段
两点,线段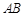 中点为
中点为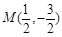 .
.
(1)求椭圆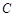 的方程;
的方程;
(2)求直线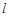 的方程;
的方程;
(3)记椭圆在直线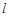 下方的部分与线段
下方的部分与线段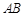 所围成的平面区域(含边界)为
所围成的平面区域(含边界)为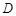 ,若曲线
,若曲线
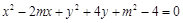 与区域
与区域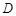 有公共点,试求
有公共点,试求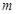 的最小值.
的最小值.
【答案】
(1)
解得: ,椭圆方程为
,椭圆方程为
(2)①当斜率 不存在时,由于点
不存在时,由于点 不是线段
不是线段 的中点,所以不符合要求;
的中点,所以不符合要求;
②设直线 方程为
方程为 ,代入椭圆方程整理得
,代入椭圆方程整理得


解得
所以直线
(3)化简曲线方程得: ,是以
,是以 为圆心,
为圆心, 为半径的圆。当圆与直线相切时,
为半径的圆。当圆与直线相切时, ,此时为
,此时为 ,圆心
,圆心 。
。
由于直线与椭圆交于 ,
,
故当圆过 时,
时, 最小。此时,
最小。此时, 。
。
【解析】略

练习册系列答案
相关题目
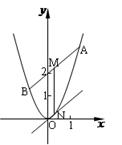
 中,已知过点
中,已知过点 的直线与线段
的直线与线段 分别相交于点
分别相交于点 。若
。若 。
。 与
与 的关系为
的关系为 ;
; ,定义函数
,定义函数 ,点列
,点列 在函数
在函数 的图像上,且数列
的图像上,且数列 是以首项为1,公比为
是以首项为1,公比为 的等比数列,
的等比数列, 为原点,令
为原点,令 ,是否存在点
,是否存在点
 ,使得
,使得 ?若存在,请求出
?若存在,请求出 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。 为
为 上偶函数,当
上偶函数,当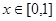 时
时 ,又函数
,又函数 对称, 当方程
对称, 当方程 在
在 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数 的取值范围。
的取值范围。 (3)是否存在常数
(3)是否存在常数