题目内容
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)已知直线![]() :
:![]() =
=![]() +
+![]()
![]()
![]() >0
>0![]() 交抛物线C:
交抛物线C:![]() =2
=2![]()
![]()
![]() >0
>0![]() 于A、B两点,M是线段AB的中点,过M作
于A、B两点,M是线段AB的中点,过M作![]() 轴的垂线交C于点N.
轴的垂线交C于点N.
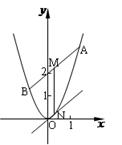
(1)若直线![]() 过抛物线C的焦点,且垂直于抛物线C的对称轴,试用
过抛物线C的焦点,且垂直于抛物线C的对称轴,试用![]() 表示|AB|;
表示|AB|;
(2)证明:过点N且与AB平行的直线![]() 和抛物线C有且仅有一个公共点;
和抛物线C有且仅有一个公共点;
(3)是否存在实数![]() ,使
,使![]() =0.若存在,求出
=0.若存在,求出![]() 的所有值;若不存在,说明理由.
的所有值;若不存在,说明理由.
(1)|AB|=2![]() (2)见解析(3)当
(2)见解析(3)当![]() ≥2
≥2![]() 时,存在实数
时,存在实数![]() =±
=±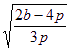 ;当
;当![]() <2
<2![]() 时,不存在实数
时,不存在实数
解析:
(1)抛物线的焦点是F![]() 0,
0,![]()
![]() ,∴
,∴![]() :
:![]() =
=![]()
![]()
![]() ,
,
则可得A、B两点坐标为![]() ±
±![]() ,
,![]()
![]() ,所以|AB|=2
,所以|AB|=2![]() .(4分)
.(4分)
(2)将![]() =
=![]() +
+![]() 代入
代入![]() =2
=2![]() 得:
得:![]() -2
-2![]() -2
-2![]() =0,
=0,
∴![]() =
=![]() =
=![]() =
=![]() ,代入
,代入![]() =2
=2![]() ,得:
,得:![]() =
=![]() ,
,
∴N![]()
![]() ,
,![]()
![]() .(7分)
.(7分)
则![]() :
:![]() -
-![]() =
=![]() ,代入
,代入![]() =2
=2![]() 得:
得:![]() -2
-2![]() +
+![]() =0,
=0,
由△=0得直线![]() 和抛物线C只有一个公共点.(10分)
和抛物线C只有一个公共点.(10分)
(3)![]() =
=![]()
![]() -
-![]() ,
,![]() -
-![]()
![]() ,
,![]() =
=![]()
![]() -
-![]() ,
,![]() -
-![]()
![]() ,
,
由![]() =0得
=0得![]()
![]() -
-![]()
![]()
![]()
![]() -
-![]()
![]() +
+![]()
![]() -
-![]()
![]()
![]()
![]() -
-![]()
![]() =0,(12分)
=0,(12分)
即![]()
![]() -
-![]()
![]()
![]()
![]() -
-![]()
![]() +
+![]()
![]() +
+![]() -
-![]()
![]()
![]()
![]() +
+![]() -
-![]()
![]() =0,
=0,
即![]() +
+![]() +
+![]() +
+![]() -
-![]() +
+![]() =0,
=0,
由(2)可得![]() +
+![]() =2
=2![]() ,
,![]()
![]() =-2
=-2![]() ,代入整理得:
,代入整理得:
3![]() +4
+4![]() +8
+8![]() -4
-4![]() =0,即
=0,即![]() =0,(16分)
=0,(16分)
由于![]() >0,
>0,![]() >0,
>0,
∴当![]() ≥2
≥2![]() 时,存在实数
时,存在实数![]() =±
=±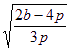 ;当
;当![]() <2
<2![]() 时,不存在实数
时,不存在实数![]() .(18分)
.(18分)

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的 (
( )都有
)都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 时
时 的周期数列,当
的周期数列,当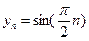 时
时 是周期为
是周期为 的周期数列。
的周期数列。 满足
满足 (
( (
( 不同时为0),且数列
不同时为0),且数列 的周期数列,求常数
的周期数列,求常数 的值;
的值; ,且
,且 .
. ,试判断数列
,试判断数列 ,试判断数列
,试判断数列 (
( ,
,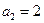 ,
, ,数列
,数列 的前
的前 ,使对任意的
,使对任意的 成立,若存在,求出
成立,若存在,求出 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的 (
( )都有
)都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 时
时 的周期数列,当
的周期数列,当 时
时 是周期为
是周期为 的周期数列。
的周期数列。 满足
满足 (
( (
(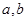 不同时为0),且数列
不同时为0),且数列 的周期数列,求常数
的周期数列,求常数 的值;
的值; ,且
,且 .
.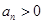 ,试判断数列
,试判断数列 ,试判断数列
,试判断数列 (
(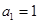 ,
,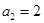 ,
, ,数列
,数列 的前
的前 ,使对任意的
,使对任意的 成立,若存在,求出
成立,若存在,求出 ,其中
,其中 .
. 时,设
时,设 ,
, ,求
,求 的解析式及定义域;
的解析式及定义域; 时,求
时,求 的最小值;
的最小值; ,当
,当 时,
时, 对任意
对任意 恒成立,求
恒成立,求 的取值范围.
的取值范围. 是等差数列,且公差为
是等差数列,且公差为 ,若数列
,若数列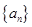 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”. ,求证:该数列是“封闭数列”;
,求证:该数列是“封闭数列”; 是否是“封闭数列”,为什么?
是否是“封闭数列”,为什么? 是数列
是数列 项和,若公差
项和,若公差 ,试问:是否存在这样的“封闭数列”,使
,试问:是否存在这样的“封闭数列”,使 ;若存在,求
;若存在,求