题目内容
描述气球膨胀状态的函数r（V）=
的导数为 ．
| 3 |
| ||
考点：导数的运算
专题：导数的概念及应用
分析：化简函数的解析式，由求导数的法则计算可得．
解答：
解：∵函数r（V）=
=
V
，
∴由求导数的法则可得r′（V）=
V-
，
故答案为：r′（V）=
V-
，
| 3 |
| ||
| 3 |
| ||
| 1 |
| 3 |
∴由求导数的法则可得r′（V）=
| 1 |
| 3 |
| 3 |
| ||
| 2 |
| 3 |
故答案为：r′（V）=
| 1 |
| 3 |
| 3 |
| ||
| 2 |
| 3 |
点评：本题考查导数的运算，属基础题．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
动点E在正方体ABCD-A1B1C1D1的棱BC上，F是CD的中点，则二面角C1-EF-C的余弦值的取值范围是（ ）
A、（0，
| ||||
B、（
| ||||
C、（0，
| ||||
D、（0，
|
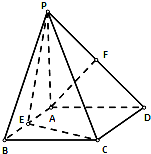如图，四棱锥P-ABCD的底面是正方形，PA⊥底面ABCD，∠PDA=45°，点E、F分别为棱AB、PD的中点．
如图，椭圆与双曲线有公共焦点F1、F2，它们在第一象限的交点为A，且AF1⊥AF2，∠AF1F2=30°，则椭圆与双曲线的离心率的倒数和为（ ）