题目内容
19.已知函数f(x)=$\left\{\begin{array}{l}2-(\frac{1}{2})^{x},&x≤0\\ 2{x}^{2}+1,&x>0\end{array}\right.$,g(x)=kx,若函数h(x)=f(x)-g(x)有3个不同的零点,则实数k的取值范围是( )| A. | (-∞,0) | B. | [2$\sqrt{2}$,+∞) | C. | (0,+∞) | D. | (2$\sqrt{2}$,+∞) |
分析 由题意可得函数f(x)的图象和函数g(x)的图象有3个不同的交点,当直线g(x)=kx和y=2x2+1(x>0)相切时,由斜率公式、导数的几何意义求得切点A的坐标,求得切线斜率的值,数形结合合可得实数k的取值范围.
解答 解:如图示: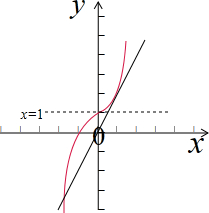
由题意可得函数f(x)的图象和函数g(x)的图象有3个不同的交点,
当直线g(x)=kx和y=2x2+1(x>0)相切时,设切点A(x0,2${{x}_{0}}^{2}$+1),
则切线的斜率k=$\frac{{{2x}_{0}}^{2}+1-0}{{x}_{0}-0}$=f′(x0)=4x0,解得 x0=$\frac{\sqrt{2}}{2}$.
此时,k=2$\sqrt{2}$,数形结合合可得函数f(x)的图象和函数g(x)的图象有3个不同的交点,
则实数k的取值范围是(2$\sqrt{2}$,+∞),
故选:D.
点评 本题主要考查函数零点个数的判断方法,体现了转化以及数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点,点D(1,0),点P,B在椭圆上,$\overrightarrow{BP}$=$\overrightarrow{DA}$.
如图,在平面直角坐标系xOy中,已知点A为椭圆$\frac{{x}^{2}}{9}$+$\frac{2{y}^{2}}{9}$=1的右顶点,点D(1,0),点P,B在椭圆上,$\overrightarrow{BP}$=$\overrightarrow{DA}$.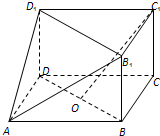 如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=4,AD=2,BB1=1,设O是线段BD的中点.
如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=4,AD=2,BB1=1,设O是线段BD的中点.