Question

圆C：（x-1）²+（y-2）²=25，直线l：（2m+1）x+（m+1）y=7m+4（m∈R）．以⊙C与直线l相交的弦为直径的圆的面积最小时圆的方程为

（x-3）²+（y-1）²=20

．

Answer 1

分析：将直线l方程化为（x+y-4）+m（2x+y-7）=0，可得l经过直线x+y-4=0与2x+y-7=0的交点P（3，1）．设⊙C与l相交于A、B两点，由平面几何知识可得当CP与l垂直时，以AB为直径的圆为所求面积最小的圆，由此利用距离公式和垂径定理加以计算，可得所求圆的方程．

解答：解：∵直线l：（2m+1）x+（m+1）y=7m+4化为（x+y-4）+m（2x+y-7）=0，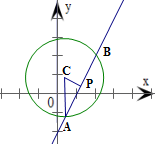
∴直线l经过直线x+y-4=0与直线2x+y-7=0的交点，
联解

x+y-4=0 2x+y-7=0

，得

x=3 y=1

，即直线l经过定点P（3，1）．
∵点P满足：（3-1）²+（1-2）²＜25，∴点P为圆C内部一点，
经过点P的直线与圆C相交，设交点为A、B，
由平面几何知识可得当CP与直线l垂直时，线段AB长达到最小值，
以AB为直径的圆为所求面积最小的圆．
∵此时|AB|=2

r2-|CP|2

=2

25-[(3-1)2+(1-2)2

 =4

5

∴圆的面积最小时，圆的半径为2

5

，可得圆的方程为（x-3）²+（y-1）²=20．
故答案为：（x-3）²+（y-1）²=20

点评：本题给出直线与圆相交，求以所得弦为一条弦的面积最小的圆的方程．着重考查了直线的方程、圆的方程和直线与圆的位置关系等知识，属于中档题．