题目内容
【题目】已知某海滨浴场海浪的高度![]() (米
(米![]() 是时刻
是时刻![]() ,单位:时)的函数,记作:
,单位:时)的函数,记作:![]() ,下表是某日各时刻的浪高数据:
,下表是某日各时刻的浪高数据:
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 |
经长期观测,![]() 的曲线可近似地看成是函数
的曲线可近似地看成是函数![]() ,
,![]() ,
,![]() 的图象.
的图象.
(![]() 的最小正周期
的最小正周期![]() ,振幅
,振幅![]() 及函数表达式;
及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的![]() 至
至![]() 之间,那个时间段不对冲浪爱好者开放?
之间,那个时间段不对冲浪爱好者开放?
【答案】(1)振幅![]() ;最小正周期
;最小正周期![]() ;函数表达式
;函数表达式![]() (2)一天内的
(2)一天内的![]() 至
至![]() 之间,
之间,![]() 至
至![]() 之间,
之间,![]() 至
至![]() 之间时间段不对冲浪爱好者开放
之间时间段不对冲浪爱好者开放
【解析】
(1)由题意可得可知![]() ,
,![]() ,
,![]() ,
,![]() ,即可求得
,即可求得![]() ;
;
(2)先阅读题意,然后解三角不等式![]() 求解即可.
求解即可.
解:(1)根据以上数据,可知![]() ,
,![]() ,
,
周期![]() .即
.即![]()
当![]() 时,可得
时,可得![]() ,
,
即![]()
![]()
![]() ,
,
![]()
故得函数表达式;![]() .
.
(2)当海浪高度高于1米时才对冲浪爱好者开放,即函数![]() 时,
时,
![]()
![]()
即![]() .
.
即![]() ,
,
即![]() ,
,
又![]() ,
,
则![]() 或
或![]() 或
或![]() .
.
则一天内的![]() 至
至![]() 之间,
之间,![]() 至
至![]() 之间,
之间,![]() 至
至![]() 之间时间段不对冲浪爱好者开放.
之间时间段不对冲浪爱好者开放.

【题目】进入高三,同学们的学习越来越紧张,学生休息和锻炼的时间也减少了.学校为了提高学生的学习效率,鼓励学生加强体育锻炼.某中学高三(3)班有学生50人.现调查该班学生每周平均体育锻炼时间的情况,得到如下频率分布直方图.其中数据的分组区间为: ![]()

(1)求学生周平均体育锻炼时间的中位数(保留3位有效数字);
(2)从每周平均体育锻炼时间在 ![]() 的学生中,随机抽取2人进行调查,求此2人的每周平均体育锻炼时间都超过2小时的概率;
的学生中,随机抽取2人进行调查,求此2人的每周平均体育锻炼时间都超过2小时的概率;
(3)现全班学生中有40%是女生,其中3个女生的每周平均体育锻炼时间不超过4小时.若每周平均体育锻炼时间超过4小时称为经常锻炼,问:有没有90%的把握说明,经常锻炼与否与性别有关?
附: 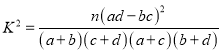
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |


