题目内容
(本小题满分12分)如图四棱锥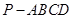 的底面是正方形,
的底面是正方形,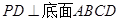 ,点E在棱PB上,O为AC与BD的交点。
,点E在棱PB上,O为AC与BD的交点。
(1)求证:平面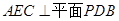 ;
;
( 2)当E为PB中点时,求证:
2)当E为PB中点时,求证: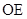 //平面PDA,
//平面PDA,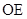 //平面PDC。
//平面PDC。
(3)当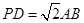 且E为PB的中点时,求
且E为PB的中点时,求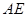 与平面
与平面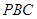 所成的角的大小。
所成的角的大小。
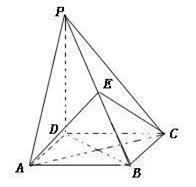
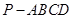 的底面是正方形,
的底面是正方形,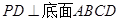 ,点E在棱PB上,O为AC与BD的交点。
,点E在棱PB上,O为AC与BD的交点。(1)求证:平面
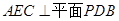 ;
;(
 2)当E为PB中点时,求证:
2)当E为PB中点时,求证: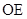 //平面PDA,
//平面PDA,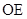 //平面PDC。
//平面PDC。(3)当
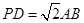 且E为PB的中点时,求
且E为PB的中点时,求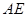 与平面
与平面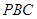 所成的角的大小。
所成的角的大小。
(1)∵四边形ABCD是正方形,∴AC⊥BD,
∵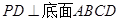 ,
,
∴PD⊥AC,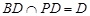
∴AC⊥平面PDB,
又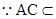 平面AEC
平面AEC
∴平面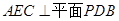 .
.
(2)∵四边形ABCD是正方形,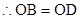 ,在
,在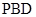 中,又
中,又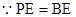
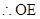 //
//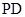 ,又
,又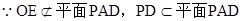
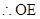 //平面PDA,同理可证
//平面PDA,同理可证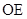 //平面PDC。
//平面PDC。
(3)∵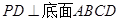 ,
,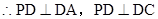 ,又
,又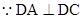
所以,可以D为坐标原点建立如图的空间直角坐标系D-xyz。设AB=1.则
D(0,0,0),A(1,0,0),C(0,1,0),B(1,1,0),P(0,0,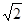 ),
),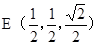
从而,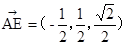 ,
,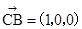 ,
,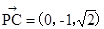
设平面PBC的一个法向量为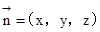 。由
。由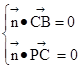 得
得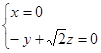
令z=1,得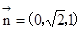 。设AE与平面PBC所成的角
。设AE与平面PBC所成的角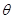 ,则
,则
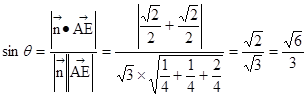
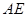 与平面PBC所成的角的正弦值为
与平面PBC所成的角的正弦值为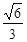 。
。
∵
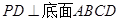 ,
,∴PD⊥AC,
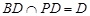
∴AC⊥平面PDB,
又
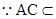 平面AEC
平面AEC ∴平面
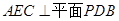 .
.(2)∵四边形ABCD是正方形,
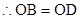 ,在
,在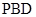 中,又
中,又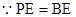
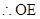 //
//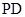 ,又
,又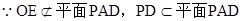
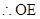 //平面PDA,同理可证
//平面PDA,同理可证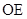 //平面PDC。
//平面PDC。(3)∵
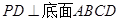 ,
,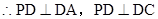 ,又
,又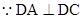
所以,可以D为坐标原点建立如图的空间直角坐标系D-xyz。设AB=1.则
D(0,0,0),A(1,0,0),C(0,1,0),B(1,1,0),P(0,0,
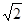 ),
),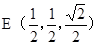
从而,
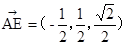 ,
,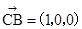 ,
,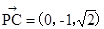
设平面PBC的一个法向量为
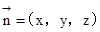 。由
。由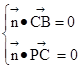 得
得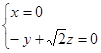
令z=1,得
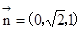 。设AE与平面PBC所成的角
。设AE与平面PBC所成的角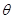 ,则
,则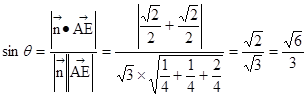
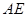 与平面PBC所成的角的正弦值为
与平面PBC所成的角的正弦值为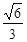 。
。略

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目




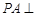 平面
平面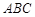 ,
,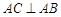 ,
,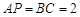 ,
,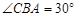 ,
,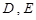 分别是
分别是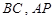 的中点.
的中点.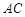 与
与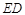 所成的角的大小;
所成的角的大小;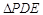 绕直线
绕直线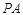 旋转一周所构成的旋转体的体积.
旋转一周所构成的旋转体的体积. ,
, ,直线
,直线 ,若
,若 ,
, ,则
,则 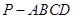 中
中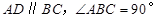 ,
,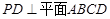 ,
,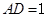 ,
,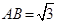 ,
,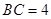 .
.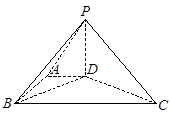
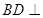
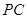 ;
;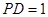 时,求此四棱锥的表面积.
时,求此四棱锥的表面积.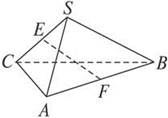
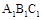 中,
中,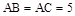 ,D,E分别为BC,
,D,E分别为BC,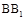 的中点,
的中点,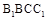 是边长为6的正方形.
是边长为6的正方形.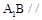 平面
平面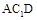 ;
;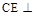 平面
平面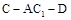 的余弦值.
的余弦值.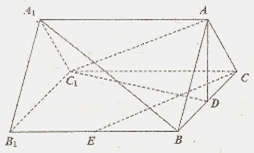
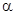 、β和不重合的直线m、n,给出下列命题:
、β和不重合的直线m、n,给出下列命题: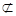
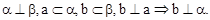
 中,点
中,点 分别在线段
分别在线段 上,且
上,且  .以下结论:①
.以下结论:① ;②
;② ;③MN//平面
;③MN//平面 ;④MN与
;④MN与 异面;⑤MN⊥平面
异面;⑤MN⊥平面 .其中有可能成立的结论的个数为( )
.其中有可能成立的结论的个数为( )