题目内容
对任意两实数a、b,定义运算“*”如下:a*b=A.(-∞,0] B.[log2![]() ,0] C.[log2
,0] C.[log2![]() ,+∞] D.R
,+∞] D.R
A
解析:本题是一个信息题,题目中涉及对数函数的概念及不等式的有关问题.注意理解题目意思,挖掘有关信息.f(x)=![]() (3x-2)*log2x
(3x-2)*log2x
当![]() (3x-2)≤log2x,即
(3x-2)≤log2x,即![]() ≤x时,
≤x时,
有f(x)=![]() (3,-2),由
(3,-2),由![]() ≤x解得x≥1,
≤x解得x≥1,
此时3x-2≥1,
所以f(x)=![]() (3x-2)≤0,此时f(x)∈(-∞,0].
(3x-2)≤0,此时f(x)∈(-∞,0].
当![]() (3x-2)>log2x时,有f(x)=log2x,
(3x-2)>log2x时,有f(x)=log2x,
此时有![]() >x,解得
>x,解得![]() <x<1,
<x<1,
所以f(x)=log2x∈(log2![]() ,0),
,0),
综上知,f(x)∈(-∞,0].

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
对任意两实数a、b,定义运算“*”如下:a*b=
则关于函数f(x)=sinx*cosx正确的命题是( )
|
| A、函数f(x)值域为[-1,1] | ||
| B、当且仅当x=2kπ(k∈Z)时,函数f(x)取得最大值1 | ||
C、函数f(x)的对称轴为x=kπ+
| ||
D、当且仅当2kπ<x<2kπ+
|
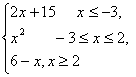 则函数f(x)=x2*[(6-x)*(2x+15)]的最大值为( )
则函数f(x)=x2*[(6-x)*(2x+15)]的最大值为( )