题目内容
如图,在边长为1的等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将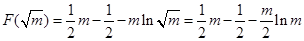 沿AF折起,得到如图所示的三棱锥
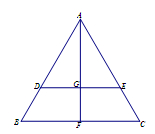
沿AF折起,得到如图所示的三棱锥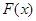 ,其中
,其中 .
.
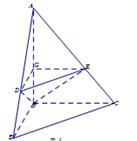
(1) 证明: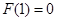 //平面
//平面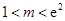 ;
;
(2) 证明: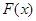
 平面
平面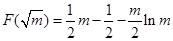 ;
;
(3)当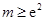 时,求三棱锥
时,求三棱锥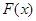 的体积
的体积
(1)详见解析;(2)详见解析;(3)
解析试题分析:(1)要证线面平行,我们可以转换为线线平行来证明;(2)要证明线面垂直,我们一般都转化为线线垂直来证明;(3)当求三棱锥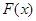 的体积困难时,我们可以考虑利用顶点转换来解决.
的体积困难时,我们可以考虑利用顶点转换来解决.
试题解析:(1)在等边三角形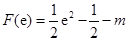 中,
中,
 ,在折叠后的三棱锥
,在折叠后的三棱锥 中
中
也成立, ,
, 平面
平面 ,
,  平面
平面 ,
, 平面
平面 ;
;
(2)在等边三角形 中,
中, 是
是 的中点,所以
的中点,所以 ①,
①, .
. 在三棱锥
在三棱锥 中,
中,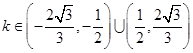 ,
,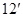 ②
②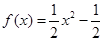 ;
;
(3)由(1)可知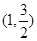 ,结合(2)可得
,结合(2)可得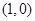
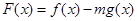
考点:(1)空间线面位置关系的证明;(2)空间向量在立体几何中的应用.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
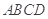 是正方形,
是正方形,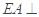 平面
平面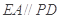 ,
,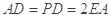 ,
,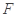 ,
,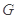 ,
, 分别为
分别为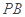 ,
,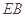 ,
,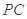 的中点.
的中点.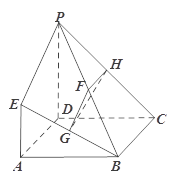
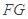
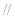 平面
平面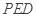 ;
;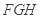 与平面
与平面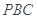 所成锐二面角的大小.
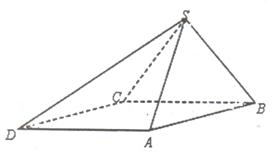
所成锐二面角的大小. 底面ABCD.已知
底面ABCD.已知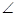 ABC=45o,AB=2,BC=2
ABC=45o,AB=2,BC=2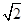 ,SA=SB=
,SA=SB=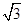 .
.
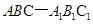 ,
,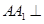 平面
平面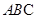 ,
,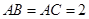 ,
,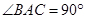 ,四边形
,四边形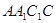 为正方形,
为正方形,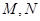 分别为
分别为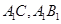 中点.
中点.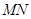 ∥面
∥面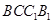 ;
; —
—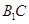 —
—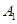 的余弦值.
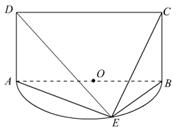
的余弦值.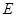 是以
是以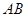 为直径的半圆
为直径的半圆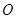 上异于
上异于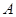 、
、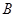 的点,矩形
的点,矩形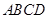 所在的平面垂直于半圆
所在的平面垂直于半圆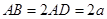 .
.
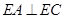 ;
;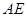 和
和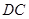 所成的角为
所成的角为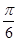 ,求平面
,求平面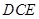 与平面
与平面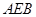 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.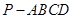 的底面为正方形,侧面
的底面为正方形,侧面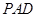
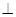 底面
底面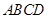 .
.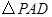 为等腰直角三角形,且
为等腰直角三角形,且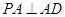 .
. ,
,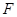 分别为底边
分别为底边 和侧棱
和侧棱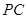 的中点.
的中点.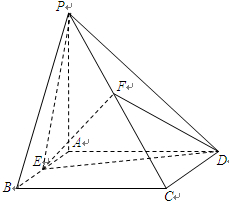
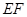 ∥平面
∥平面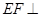 平面
平面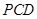 ;
; 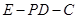 的余弦值.
的余弦值.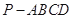 中,侧面
中,侧面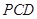
 底面
底面 ,
,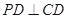 ,底面
,底面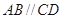 ,
,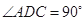 ,
,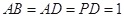 ,
,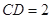 .
.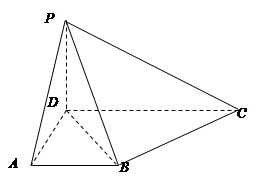
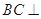 平面
平面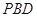 ;
;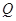 为侧棱
为侧棱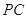 上一点,
上一点,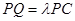 ,试确定
,试确定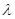 的值,使得二面角
的值,使得二面角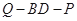 为
为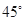 .
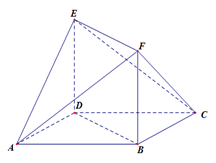
.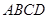 是菱形,
是菱形,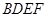 是矩形,
是矩形,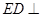 平面
平面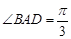 ,
,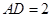 .
.
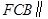 平面
平面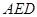 ;
;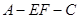 为直二面角,求直线
为直二面角,求直线 与平面
与平面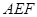 所成的角
所成的角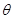 的正弦值.
的正弦值.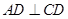 ,
,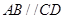 ,
,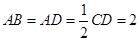 ,点M在线段EC上(除端点外)
,点M在线段EC上(除端点外)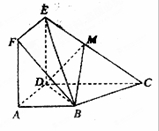
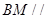 平面
平面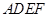 ;
;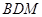 与平面ABF所成二面角为锐角,且该二面角的余弦值为
与平面ABF所成二面角为锐角,且该二面角的余弦值为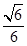 时,求三棱锥
时,求三棱锥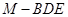 的体积
的体积