题目内容
17．双曲线x2-y2=a2（a＞0）的两个焦点分别为F1，F2，P为双曲线上任意一点，求证：|PF1|，|PO|，|PF2|成等比数列（O为坐标原点）分析 利用双曲线的第二定义，结合等比数列的性质，即可证明结论．
解答 证明：不妨设P（x，y），是左边一支的点，所以|PF2|=ex-a，|PF1|=ex+a（其中e=$\sqrt{2}$）．
所以|PF1||PF2|=e2x2-a2=2x2-（x2-y2）=x2+y2=|PO|2，
所以|PF1|，|PO|，|PF2|成等比数列（O为坐标原点）．
点评 本题考查双曲线的第二定义，等比数列的性质，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
8．为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法，某媒体在该地区选择了3600人调查，就是否“取消英语听力”的问题，调查统计的结果如下表：
已知在全体样本中随机抽取1人，抽到持“应该保留”态度的人的概率为0.05．
（1）现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈，问应在持“无所谓”态度的人中抽取多少人？
（2）在持“应该保留”态度的人中，用分层抽样的方法抽取6人平均分成两组进行深入交流，求第一组中在校学生人数ξ的分布列和数学期望．
| 应该取消 | 应该保留 | 无所谓 | |
| 在校学生 | 2100人 | 120人 | y人 |
| 社会人士 | 600人 | x人 | z人 |
（1）现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈，问应在持“无所谓”态度的人中抽取多少人？
（2）在持“应该保留”态度的人中，用分层抽样的方法抽取6人平均分成两组进行深入交流，求第一组中在校学生人数ξ的分布列和数学期望．
2．奇函数y=f（x）在区间[3，7]上是增函数，且最小值为-5，那么f（x）在区间[-7，-3]上（ ）
| A． | 是增函数且最小值为5 | B． | 是增函数且最大值为5 | ||
| C． | 是减函数且最小值为5 | D． | 是减函数且最大值为5 |
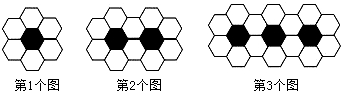用黑白两种正六边形瓷砖按如图所示规律拼成若干图案．