题目内容
在△ABC中,角A,B,C所对的边长分别为a,b,c,且asinAsinB+bcos2A= a,则
a,则 的值为
的值为
| A.1 | B. | C. | D.2 |
B
解析试题分析:因为asinAsinB+bcos2A= a,所以由正弦定理得
a,所以由正弦定理得 ,即
,即 ,所以
,所以 =
= 。
。
考点:本题主要考查正弦定理的应用。
点评:基础题,三角形问题,多是利用正弦定理、余弦定理实施边角转化。本题还利用了方程思想。

练习册系列答案
相关题目
 中,若
中,若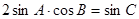 ,则
,则 的形状为( )
的形状为( )
| A.直角三角形 | B.等边三角形 | C.等腰三角形 | D.等腰直角三角形 |
在△ABC中,A=60°,C=45°,b=2,则此三角形的最小边长为( )
| A.2 | B.2 -2 -2 | C. -1 -1 | D.2( -1) -1) |
△ABC中,∠C=90°,且CA=CB=3,点M满足
 ,则
,则 =
=
| A.18 | B.3 | C.15 | D.9 |
在 中,若
中,若
 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
在 中,
中, 分别为角
分别为角 所对边,若1+cosA=2sinBsinC,则此三角形一定是( )
所对边,若1+cosA=2sinBsinC,则此三角形一定是( )
| A.等腰直角三角形 | B.等腰或直角三角形 |
| C.等腰三角形 | D.直角三角形 |
已知 中,
中, 所对的边分别为
所对的边分别为 ,且
,且 ,那么角
,那么角 等于( )
等于( )
A. | B. | C. | D. |
满足条件 的
的 的个数是( )
的个数是( )
| A.零个 | B.一个 | C.两个 | D.无数个 |
在 中,若
中,若 ,则这个三角形一定是( )
,则这个三角形一定是( )
| A.等腰三角形 | B.直角三角形 | C.等腰直角三角形 | D.等边三角形 |