题目内容
在 中,
中, 分别为角
分别为角 所对边,若1+cosA=2sinBsinC,则此三角形一定是( )
所对边,若1+cosA=2sinBsinC,则此三角形一定是( )
| A.等腰直角三角形 | B.等腰或直角三角形 |
| C.等腰三角形 | D.直角三角形 |
C
解析试题分析:因为 ,所以
,所以 ,又cos(B+C)=-cosA,所以cos (B-C)=1,所以B=C.因此选C 。
,又cos(B+C)=-cosA,所以cos (B-C)=1,所以B=C.因此选C 。
考点:和差公式;三角形形状的判断。
点评:在解三角形时,我们要注意三角形内的隐含条件: ;
; 。
。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在 中,
中, ,
, ,则
,则 的面积为( )
的面积为( )
A. | B. | C. | D. |
△ABC中,若b=6,c=10,B=30°,则解此三角形的结果为( )
| A.无解 | B.有一解 | C.有两解 | D.一解或两解 |
如果 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于 的三个内角的正弦值,则( )
的三个内角的正弦值,则( )
A. 和 和 都是锐角三角形 都是锐角三角形 |
B. 和 和 都是钝角三角形 都是钝角三角形 |
C. 是钝角三角形, 是钝角三角形, 是锐角三角形 是锐角三角形 |
D. 是锐角三角形, 是锐角三角形, 是钝角三角形 是钝角三角形 |
△ABC的三个内角 所对的边分别为
所对的边分别为 ,
, ,则
,则
A. | B. | C. | D. |
在 中,若
中,若 ,则
,则 的形状一定是( )
的形状一定是( )
| A.等腰三角形 | B.直角三角形 |
| C.等腰直角三角形 | D.等边三角形 |
已知△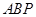 的顶点
的顶点 、
、 分别为双曲线
分别为双曲线 的左右焦点,顶点
的左右焦点,顶点 在双曲线
在双曲线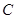 上,则
上,则 的值等于
的值等于
A. | B. | C. | D. |
 a,则
a,则 的值为
的值为
 B.
B. C.
C. D.
D.