题目内容
(12分)设数列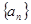 的前
的前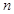 项和为
项和为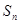 ,
,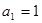 ,且对任意正整数
,且对任意正整数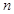 ,点
,点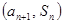 在直线
在直线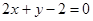 上.
上.
(Ⅰ) 求数列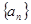 的通项公式;
的通项公式;
(Ⅱ)是否存在实数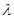 ,使得数列
,使得数列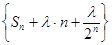 为等差数列?若存在,求出
为等差数列?若存在,求出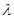 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
【答案】
.解:(Ⅰ)由题意可得:
 ①
①
 时,
时,  ②
②
①─②得 ,
,


 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列,
(Ⅱ)解法一:
若 为等差数列,
为等差数列,
则 成等差数列,
成等差数列,


得
又 时,
时, ,显然
,显然 成等差数列,
成等差数列,
故存在实数 ,使得数列
,使得数列 成等差数列.
成等差数列.
解法二: 

欲使 成等差数列,只须
成等差数列,只须 即
即 便可.
便可.
故存在实数 ,使得数列
,使得数列 成等差数列.
成等差数列.
【解析】略

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
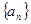 的各项均为正数,
的各项均为正数,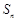 为其前
为其前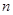 项和,对于任意
项和,对于任意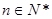 ,总有
,总有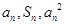 成等差数列.
成等差数列.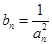 ,数列
,数列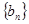 的前
的前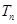 ,求证:
,求证: .
. 的前
的前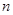 项和为
项和为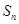 ,且满足
,且满足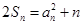 ,
,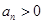 ,
,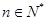 .
.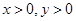 ,且
,且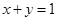 ,证明:
,证明: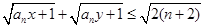 .
.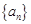 的前
的前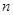 项和为
项和为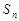 ,若对任意
,若对任意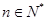 ,都有
,都有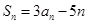 .
.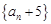 是等比数列,并求数列
是等比数列,并求数列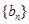 满足
满足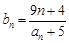 ,问是否存在
,问是否存在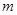 ,使得
,使得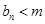 恒成立?如果存在,求出
恒成立?如果存在,求出