题目内容
已知函数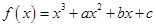 ,当
,当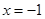 时,取得极大值
时,取得极大值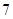 ;当
;当 时,取得极小值.
时,取得极小值.
求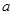 、
、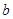 、
、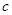 的值;
的值;
求 在
在 处的切线方程.
处的切线方程.
(1)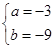 ,
,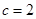
(2)
解析试题分析:解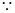
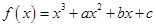 ,
,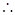
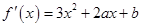
由题意知,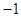 和
和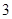 是方程
是方程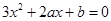 的两个实数根
的两个实数根
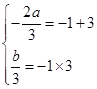 ,解得:
,解得: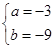
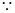
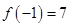
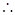
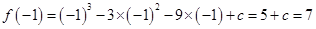 ,所以
,所以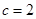 。
。
由(1)可知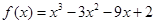 ,
,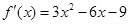
所以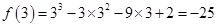 ,
,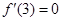
 在
在 处的切线方程为
处的切线方程为
考点:导数的几何意义
点评:主要是考查了导数的几何意义来求解切线方程以及导数的计算,属于基础题。

练习册系列答案
相关题目
题目内容
已知函数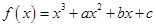 ,当
,当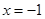 时,取得极大值
时,取得极大值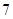 ;当
;当 时,取得极小值.
时,取得极小值.
求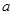 、
、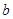 、
、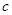 的值;
的值;
求 在
在 处的切线方程.
处的切线方程.
(1)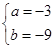 ,
,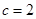
(2)
解析试题分析:解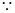
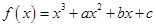 ,
,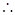
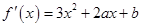
由题意知,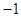 和
和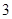 是方程
是方程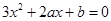 的两个实数根
的两个实数根
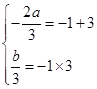 ,解得:
,解得: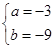
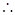
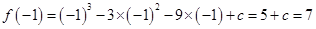 ,所以
,所以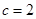 。
。
由(1)可知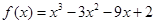 ,
,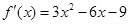
所以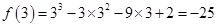 ,
,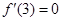
 在
在 处的切线方程为
处的切线方程为
考点:导数的几何意义
点评:主要是考查了导数的几何意义来求解切线方程以及导数的计算,属于基础题。
