题目内容
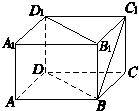
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=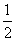 AD.
AD.
(1)求异面直线BF与DE所成的角的大小;
(2)证明平面AMD⊥平面CDE;
(2)求二面角ACDE的余弦值.
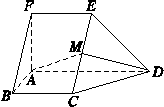
解 如图所示,建立空间直角坐标系,点A为坐标原
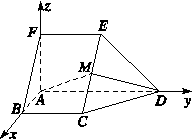 点.
点.
设AB=1,依题意得B(1,0,0),
C(1,1,0),D(0,2,0),E(0,1,1),F(0,0,1),
M(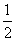 ,1,
,1,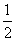 ).
).
(1) 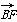 =(-1,0,1),
=(-1,0,1),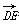 =(0,-1,1),
=(0,-1,1),
于是cos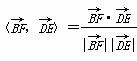 =
= =
=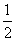 .
.
所以异面直线BF与DE所成的角的大小为60°.
(2)证明 由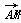 =(
=(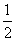 ,1,
,1,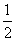 ),
),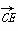 =(-1,0,1),
=(-1,0,1),
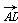 =(0,2,0),可得
=(0,2,0),可得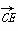 ·
·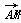 =0,
=0,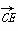 ·
·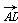 =0.
=0.
因此,CE⊥AM,CE⊥AD.
又AM∩AD=A,故CE⊥平面AMD.
而CE⊂平面CDE,所以平面AMD⊥平面CDE.
(3)设平面CDE的法向量为u=(x,y,z),
则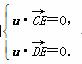
于是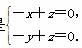 令x=1,可得u=(1,1,1).
令x=1,可得u=(1,1,1).
又由题设,平面ACD的一个法向量为v=(0,0,1).
所以,cos〈u,v〉=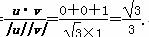
因为二面角ACDE为锐角,所以其余弦值为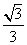 .
.

练习册系列答案
相关题目
 的公比
的公比 ,前
,前 项的和为
项的和为 .令
.令 ,数列
,数列 的前
的前 项和为
项和为 ,若
,若 对
对 恒成立,则实数
恒成立,则实数 的最小值为 .
的最小值为 .  ,
, ,则
,则 的值是( )
的值是( ) B.-
B.-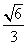 B.
B.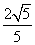
 D.
D.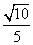
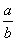 =-3;
=-3;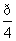 -2x)的单调增区间是 ( )
-2x)的单调增区间是 ( )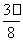 , kπ+
, kπ+ ,
,  kπ+
kπ+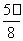 ] (k∈Z)
] (k∈Z) 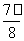 ] (k∈Z)
] (k∈Z) 的图象先向右平移
的图象先向右平移 个单位,然后向下平移2个单位后所得的函数解析式为________________________________
个单位,然后向下平移2个单位后所得的函数解析式为________________________________
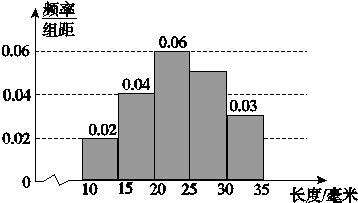
 等品.用频率估计概率,现从该批产品中随机抽取1件,则其为二等品的概率是( )
等品.用频率估计概率,现从该批产品中随机抽取1件,则其为二等品的概率是( )