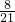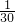题目内容
已经一组函数y=2sin（ωx+φ）（ω＞0，0＜φ≤2π）），其中ω在集合{2，3，4}中任取一个数，ϕ在集合{
，
，
，π，
，
，2π}中任取一个数．从这些函数中任意抽取两个，其图象能经过相同的平移后得到函数y=2sinωx的图象的概率是（ ）A．
B．
C．
D．
【答案】分析：确定从中任意抽取两个函数的方法数，再考虑向右平移
、
、
、
个单位得到函数y=2sinωx的图象的方法数，利用古典概型的概率公式，即可求得结论．
解答：解：这一组函数共有3×7=21个，从中任意抽取两个函数共有
=210种不同的方法，其中从这些函数中任意抽取两个，向右平移
个单位得到函数y=2sinωx的图象有3种取法；向右平移
个单位得到函数y=2sinωx的图象也有3种取法；向右平移
个单位得到函数y=2sinωx的图象有1种取法；向右平移
个单位得到函数y=2sinωx的图象也有1种取法；
故所求概率是
=
故选C．
点评：本题考查古典概型的概率，考查学生的计算能力，属于基础题．
、、、个单位得到函数y=2sinωx的图象的方法数，利用古典概型的概率公式，即可求得结论．解答：解：这一组函数共有3×7=21个，从中任意抽取两个函数共有
=210种不同的方法，其中从这些函数中任意抽取两个，向右平移个单位得到函数y=2sinωx的图象有3种取法；向右平移个单位得到函数y=2sinωx的图象也有3种取法；向右平移个单位得到函数y=2sinωx的图象有1种取法；向右平移个单位得到函数y=2sinωx的图象也有1种取法；故所求概率是
=故选C．
点评：本题考查古典概型的概率，考查学生的计算能力，属于基础题．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
相关题目
在集合
中任取一个数，j在集合{
，
，
，π，
，
，2π}中任取一个数.从这些函数中任意抽取两个，其图象能经过相同的平移后得到函数y＝2sinωx的图象的概率是 ( )
B．
C．
D．
，
，
，π，
，
，2π}中任取一个数．从这些函数中任意抽取两个，其图象能经过相同的平移后得到函数y=2sinωx的图象的概率是
