题目内容
(本小题满分14分)
如图,斜三棱柱 中,侧面
中,侧面
 底面ABC,侧面
底面ABC,侧面 是菱形,
是菱形, ,E、F分别是
,E、F分别是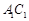 、AB的中点.
、AB的中点.
求证:(1)EF∥平面 ;
;
(2)平面CEF⊥平面ABC.
证明:取BC中点M,连结FM, .在△ABC中,因为F,M分别为BA,BC的中点,所以FM
.在△ABC中,因为F,M分别为BA,BC的中点,所以FM 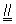
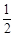 AC.因为E为
AC.因为E为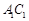 的中点,AC
的中点,AC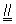
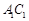 ,所以FM
,所以FM 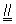
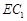 .从而四边形
.从而四边形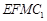 为平行四边形,所以
为平行四边形,所以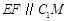 .所以EF∥平面
.所以EF∥平面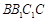 . (2) 在平面
. (2) 在平面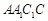 内,作
内,作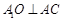 ,O为垂足。因为∠
,O为垂足。因为∠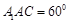 ,所以
,所以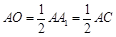 ,从而O为AC的中点. 所以
,从而O为AC的中点. 所以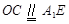 ,因而
,因而 .因为侧面
.因为侧面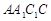 ⊥底面ABC,交线为AC,
⊥底面ABC,交线为AC,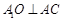 ,所以
,所以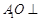 底面ABC.所以
底面ABC.所以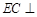 底面ABC.又因为
底面ABC.又因为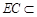 平面EFC, 所以平面CEF⊥平面ABC.
平面EFC, 所以平面CEF⊥平面ABC.
解析
试题分析:证明:(1)取BC中点M,连结FM, .
.
在△ABC中,因为F,M分别为BA,BC的中点,
所以FM 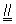
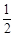 AC. ………………………………2分
AC. ………………………………2分
因为E为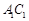 的中点,AC
的中点,AC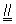
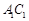 ,所以FM
,所以FM 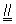
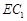 .
.
从而四边形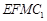 为平行四边形,所以
为平行四边形,所以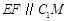 .……………………4分
.……………………4分
又因为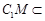 平面
平面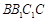 ,
,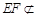 平面
平面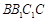 ,
,
所以EF∥平面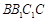 .…………………6分
.…………………6分
(2) 在平面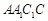 内,作
内,作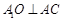 ,O为垂足.
,O为垂足.
因为∠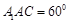 ,所以
,所以 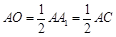 ,
,
从而O为AC的中点.……8分
所以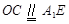 ,因而
,因而 . …………………10分
. …………………10分
因为侧面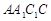 ⊥底面ABC,交线为AC,
⊥底面ABC,交线为AC,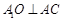 ,所以
,所以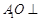 底面ABC.
底面ABC.
所以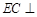 底面ABC. …………………………………………12分
底面ABC. …………………………………………12分
又因为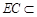 平面EFC,所以平面CEF⊥平面ABC.………………14分
平面EFC,所以平面CEF⊥平面ABC.………………14分
考点:本题考查了空间中的线面关系
点评:证明立体几何问题常常利用几何方法,通过证明或找到线面之间的关系,依据判定定理或性质进行证明求解

练习册系列答案
相关题目
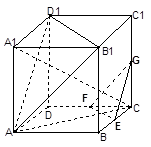
 的底面是正六边形,
的底面是正六边形, 平面
平面 ,
, 是
是 的中点。
的中点。
 //平面
//平面 ;
; ,当二面角
,当二面角 的大小为
的大小为 时,求
时,求 的值。
的值。 中,
中,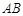 ∥
∥ ,
, ,
, ,
,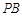 ⊥
⊥ ,
, ⊥
⊥ 为
为 的中点.
的中点.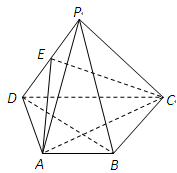
 ∥平面
∥平面 ;
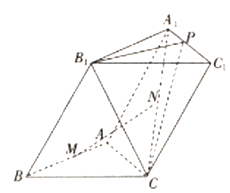
; .
.
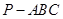 中,
中,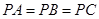 ,
,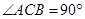 ,
,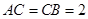 .
. 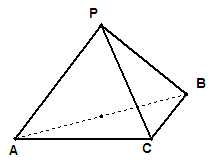
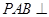 平面
平面 ;
;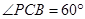 时,求三棱锥
时,求三棱锥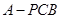 的体积.
的体积. 平面CC1D1D,且PC=PD=
平面CC1D1D,且PC=PD= .
.
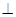 平面PBC;
平面PBC; ,当a为何值时,PC//平面
,当a为何值时,PC//平面 .
. 的菱形
的菱形 中,
中, ,
, 面
面 ,
, 、
、 分别是
分别是 和
和 的中点.
的中点.
 面
面 ;
;  ⊥平面
⊥平面 ;
; 与平面
与平面 ABC=60
ABC=60 ,EC
,EC 面ABCD,FA
面ABCD,FA