题目内容
设f(x)在x=1处连续,且![]()
![]() =2,求f′(1).
=2,求f′(1).
∵f(x)在x=1处连续, ∴![]() f(x)=f(1). 2分
f(x)=f(1). 2分
又![]() f(x)=
f(x)=![]() (x-1)·
(x-1)·![]() =
=![]() (x-1)·
(x-1)·![]()
![]() =0·2=0.
=0·2=0.
∴f(1)=0. 6分
根据导数的定义,得
f′(1)=![]()
![]() =
=![]()
![]() =2. 10分
=2. 10分
解析:
本题考查抽象函数在某点处的导数.根据f(x)在某点连续的定义及导数的定义求解.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
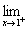 试讨论当a、b为何值时,f(x)在x=1处可导.
试讨论当a、b为何值时,f(x)在x=1处可导.