题目内容
7.已知函数$f(x)=\left\{\begin{array}{l}sinπx\;,\;\;-1≤x<0\\ f({x-1})+1\;,\;\;x≥0\end{array}\right.$.当x∈[n,n+1),n≥-1,n∈Z时,用x和n表示的f(x)=sin[(x-n-1)]π+n+1.分析 x∈[n,n+1),则x-n-1∈[-1,0),f(x-n-1)=sin[(x-n-1)]π,利用x≥0,f(x-1)=f(x)-1,可得f(x)-n-1=sin[(x-n-1)]π,即可得出结论.
解答 解:x∈[n,n+1),则x-n-1∈[-1,0),f(x-n-1)=sin[(x-n-1)]π,
∵x≥0,f(x-1)=f(x)-1,
∴f(x)-n-1=sin[(x-n-1)]π,
∴f(x)=sin[(x-n-1)]π+n+1,
故答案为sin[(x-n-1)]π+n+1.
点评 本题考查函数的解析式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
18.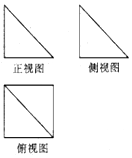 如图所示,某几何体的三视图中,正视图和侧视图都是腰长为1的等腰直角三角形,则该几何体的体积为( )
如图所示,某几何体的三视图中,正视图和侧视图都是腰长为1的等腰直角三角形,则该几何体的体积为( )
 如图所示,某几何体的三视图中,正视图和侧视图都是腰长为1的等腰直角三角形,则该几何体的体积为( )
如图所示,某几何体的三视图中,正视图和侧视图都是腰长为1的等腰直角三角形,则该几何体的体积为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | $1+\sqrt{2}$ |
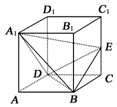 如图所示,在正方体ABCD-A1B1C1D1中,已知E为棱CC1上的动点.
如图所示,在正方体ABCD-A1B1C1D1中,已知E为棱CC1上的动点.