题目内容
14．计算：$\underset{lim}{x-∞}$（1+$\frac{1}{2x}$）x+2．分析 化简$\underset{lim}{x-∞}$（1+$\frac{1}{2x}$）x+2=$\underset{lim}{x-∞}$（1+$\frac{1}{2x}$）x（1+$\frac{1}{2x}$）2=$\underset{lim}{x-∞}$（1+$\frac{1}{2x}$）x=$\underset{lim}{x-∞}$[（1+$\frac{1}{2x}$）2x]${\;}^{\frac{1}{2}}$=$\sqrt{e}$．
解答 解：$\underset{lim}{x-∞}$（1+$\frac{1}{2x}$）x+2
=$\underset{lim}{x-∞}$（1+$\frac{1}{2x}$）x（1+$\frac{1}{2x}$）2
=$\underset{lim}{x-∞}$（1+$\frac{1}{2x}$）x
=$\underset{lim}{x-∞}$[（1+$\frac{1}{2x}$）2x]${\;}^{\frac{1}{2}}$
=$\sqrt{e}$．
点评 本题考查了极限的求法及化简应用．
练习册系列答案
相关题目
如图，在四棱锥P-ABCD中，底面是边长为2$\sqrt{3}$的菱形，且∠BAD=120°，且PA⊥平面ABCD，PA=2$\sqrt{6}$，M，N分别为PB，PD的中点．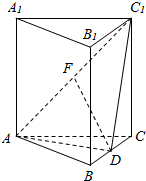
如图，在直三棱柱ABC-A1B1C1中，AB=AC，BD=DC，AF=C1F．