题目内容
4．函数f（x）=x2+bx+c，若f（3）=f（5），则b=-8．分析 利用二次函数的对称轴直接求解即可．
解答 解：函数f（x）=x2+bx+c，若f（3）=f（5），
可知二次函数的对称轴为：x=4，
所以$-\frac{b}{2}=4$，解得b=-8．
故答案为：-8．
点评 本题考查二次函数的简单性质的应用，考查计算能力．
练习册系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
在三棱锥P-ABC中，PA⊥面ABC，∠ABC=90°，若AD⊥PB，垂足为D，求证：AD⊥面BPC．
12．
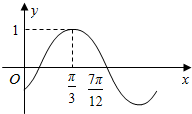已知函数y=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则 （ ）
已知函数y=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则 （ ）| A． | ω=1，φ=$\frac{π}{6}$ | B． | ω=1，φ=-$\frac{π}{6}$ | C． | ω=2，φ=$\frac{π}{6}$ | D． | ω=2，φ=-$\frac{π}{6}$ |
13．函数f（x）=sin（x+$\frac{π}{6}$）的一个递减区间是（ ）
| A． | [-$\frac{π}{2}$，$\frac{π}{2}$] | B． | [-π，0] | C． | [-$\frac{2}{3}π$，$\frac{2}{3}π$] | D． | [$\frac{π}{2}$，$\frac{2}{3}π$] |